Motivations

Non-linear Hypothesis

  • Representation

    • Problem

    • For non-linear classification, hypothesis is a high order polynomial

      • if it is a quadratic function of 100 features, hypothesis will be close to 5000 features

        • Time Complexity is O ( n^2 )

      • if it is a cubic function of 100 features, hypothesis will be close to 1,70,000

    Problem.png

  • Computer Vision

    • Why it is hard ?

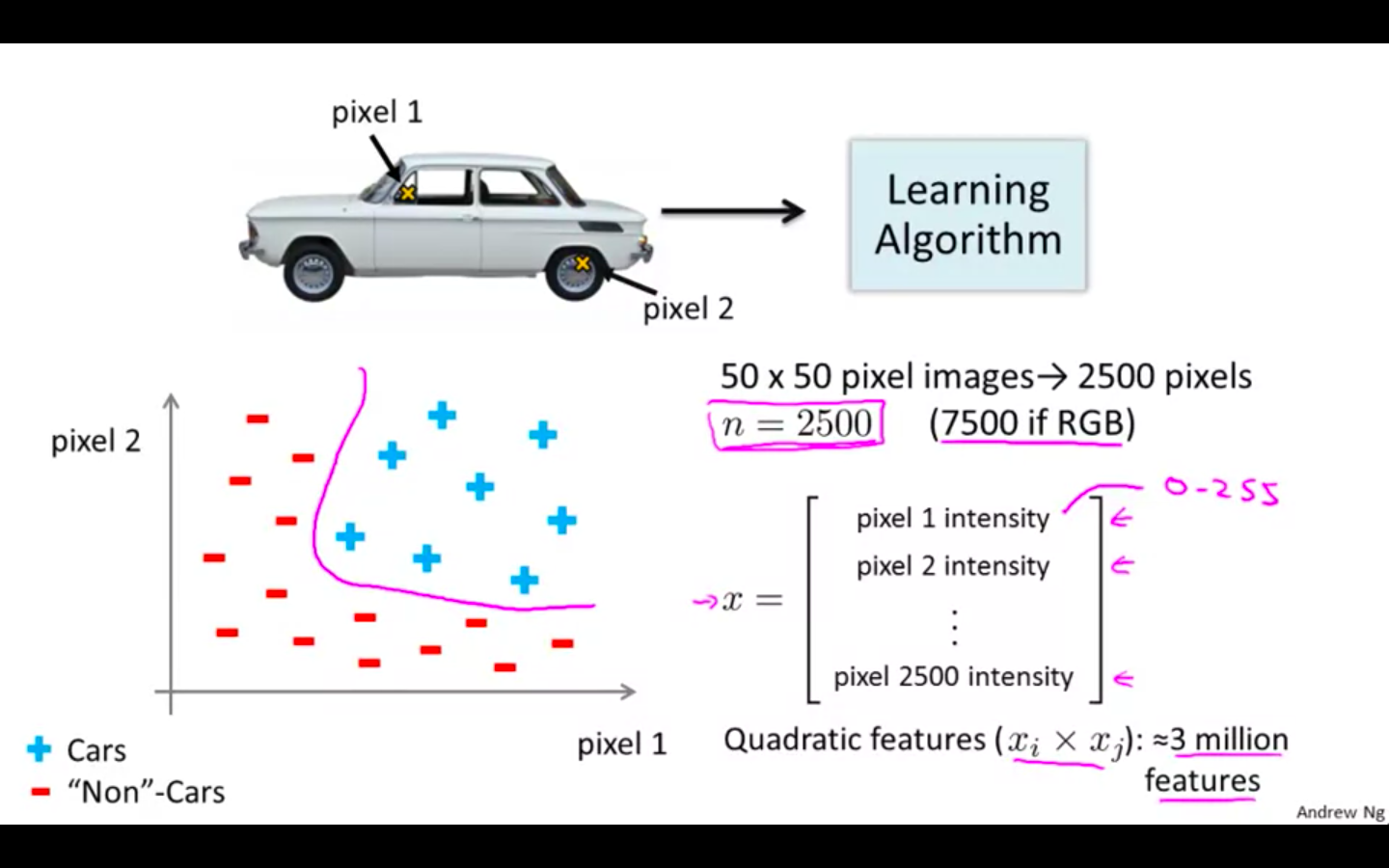
      • Computer see the matrix of pixel density of the image

      Computer Vision Example.png

    • How does it work?

      • We give the classifier image of cars with labels and not images of cars with labels, it train on them.

      • We give a test image to predict, if it’s a car or not car.

      Computer Vision Example 1.png

    • If we have 50 x 50 pixels images, then the n will 2500 ( greyscale ) 7500 ( RGB )

    Computer Vision Example 2.png

    Neurons and the Brain

    • Neural Networks

      • Origin: Algorithms that try to mimic the brain

      Neural Networks.png

    • Neural Rewiring Experiments

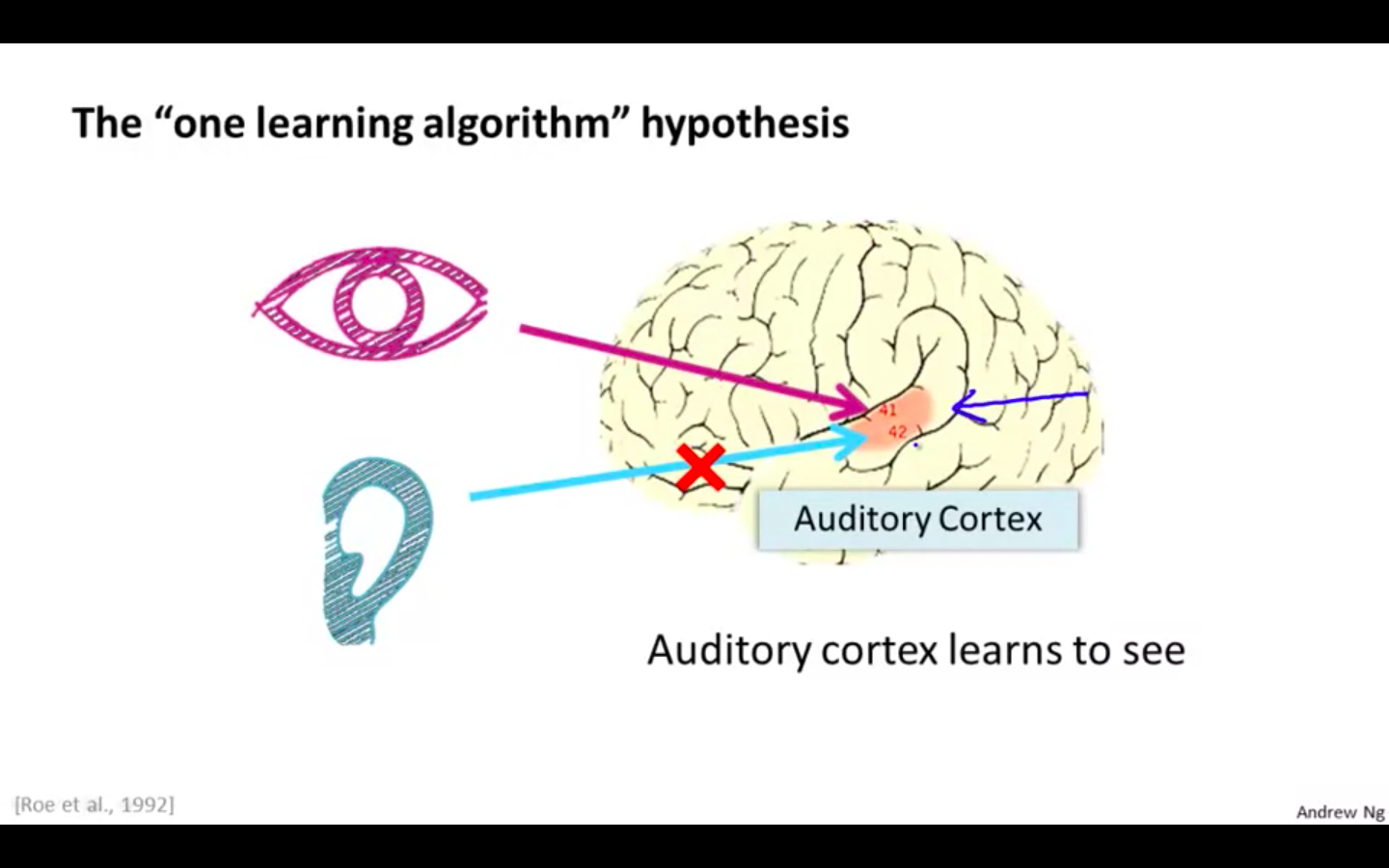
      • Rewiring the auditory cortex with eyes rather than ears, it learns to see or visual discrimination with that tissue

      Experiment 1.png

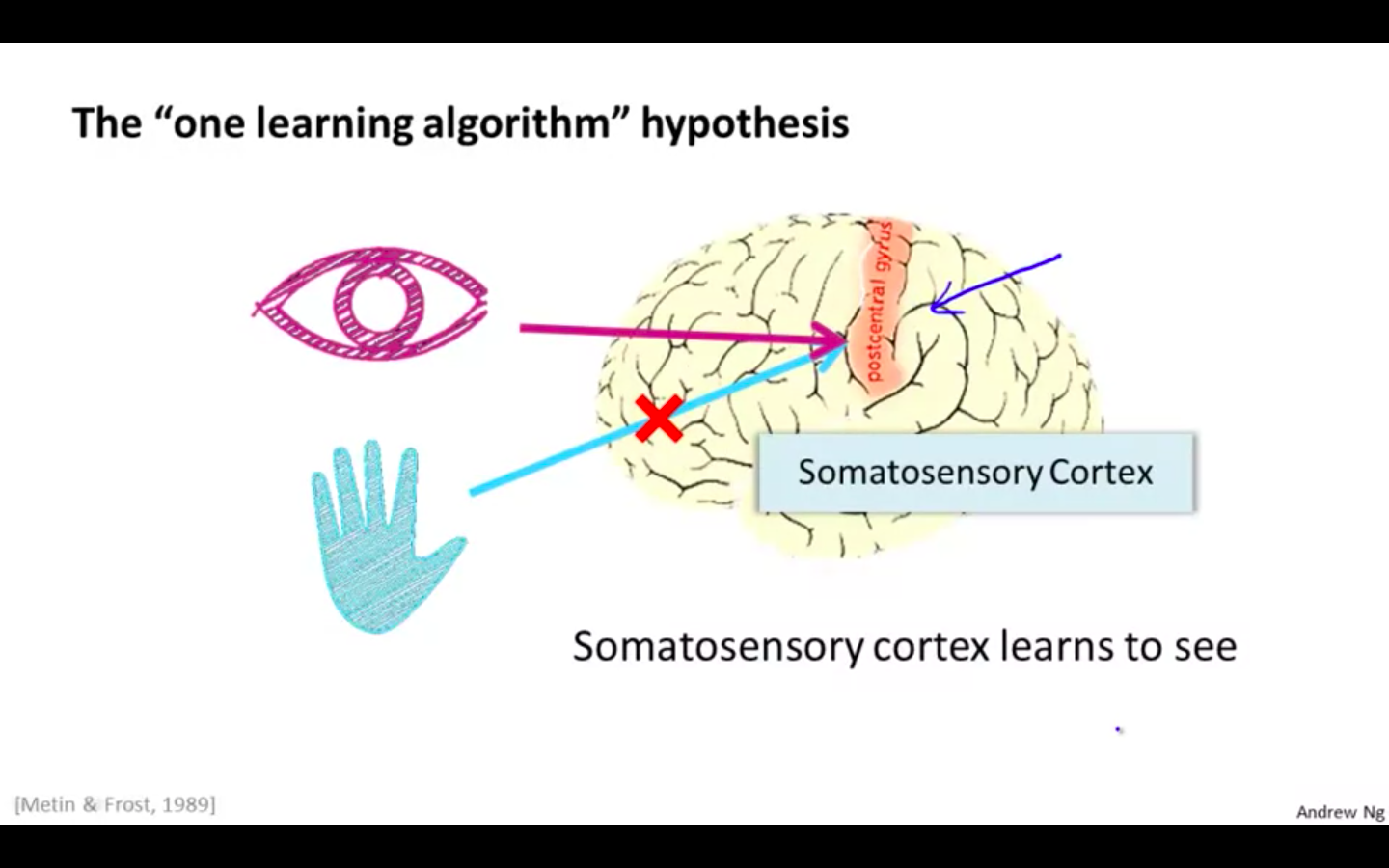
      • In the same way, by rewiring the somatosensory cortex with the eyes rather than the hands, it learns to visual discrimination with that tissue

      Experiment 2.png

      • It is “ one learning algorithm “, whatever input it receives it generalises it perform that particular task.

    • Examples

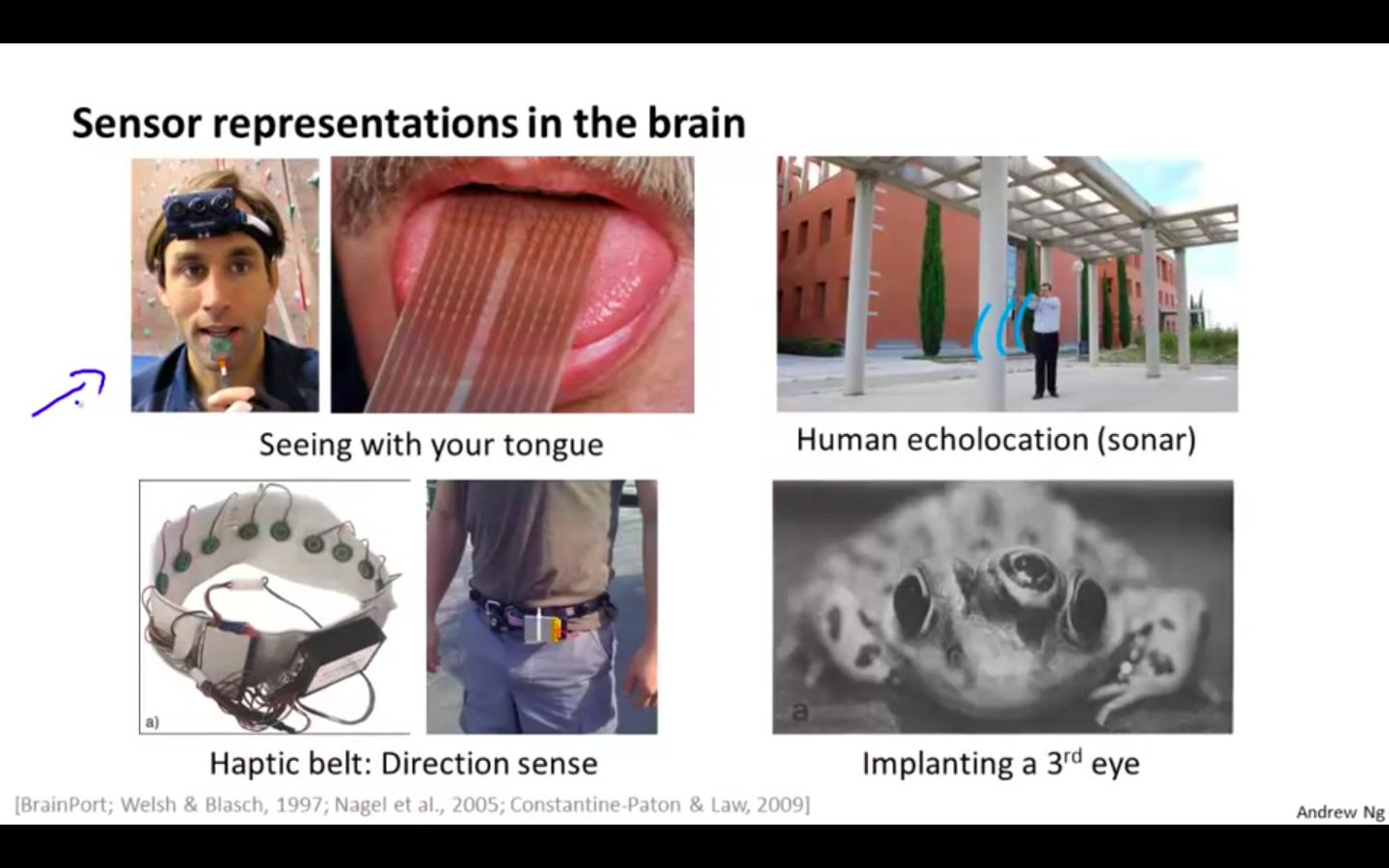
      • Seeing with your tongue

      • Human echolocation

      • Haptic Belt

      • Implementing 3rd eye in the frog

      Examples.png

    Neural Networks

    Model Representation 1

    • Neurons

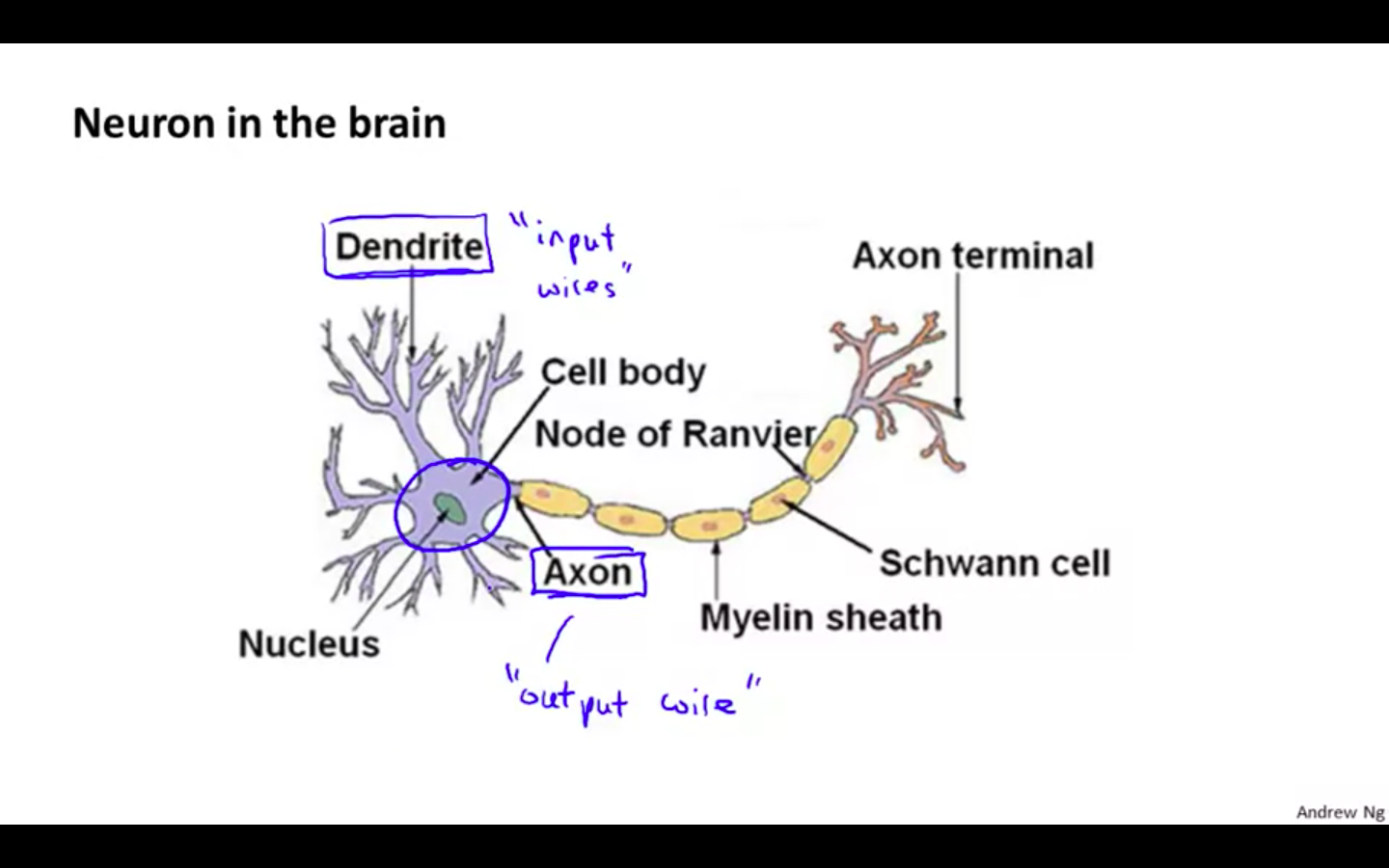
      • There are input wires called ‘Dendrites’.

      • There are output wire called ‘Axon’

      • There is also cell body and nucleus

      Neuron Diagram.png

      • Working of a Neuron

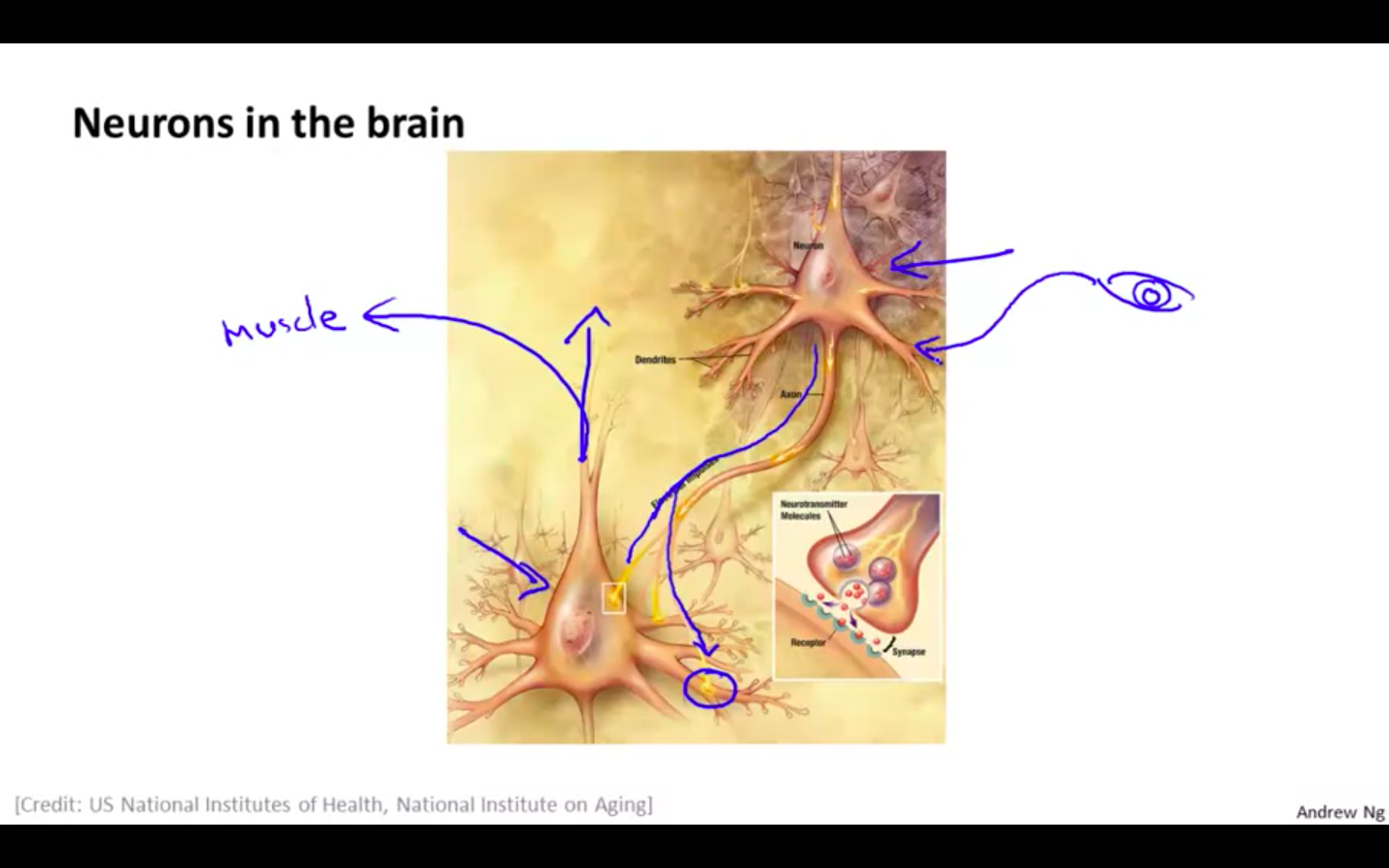
        • One neuron sends information to other neuron by sending electric pulses ( called “spikes” )

        • Axon terminal of one neuron is connected to the dendrites of the other neuron

        Working - Neuron.png

    • Neuron Model

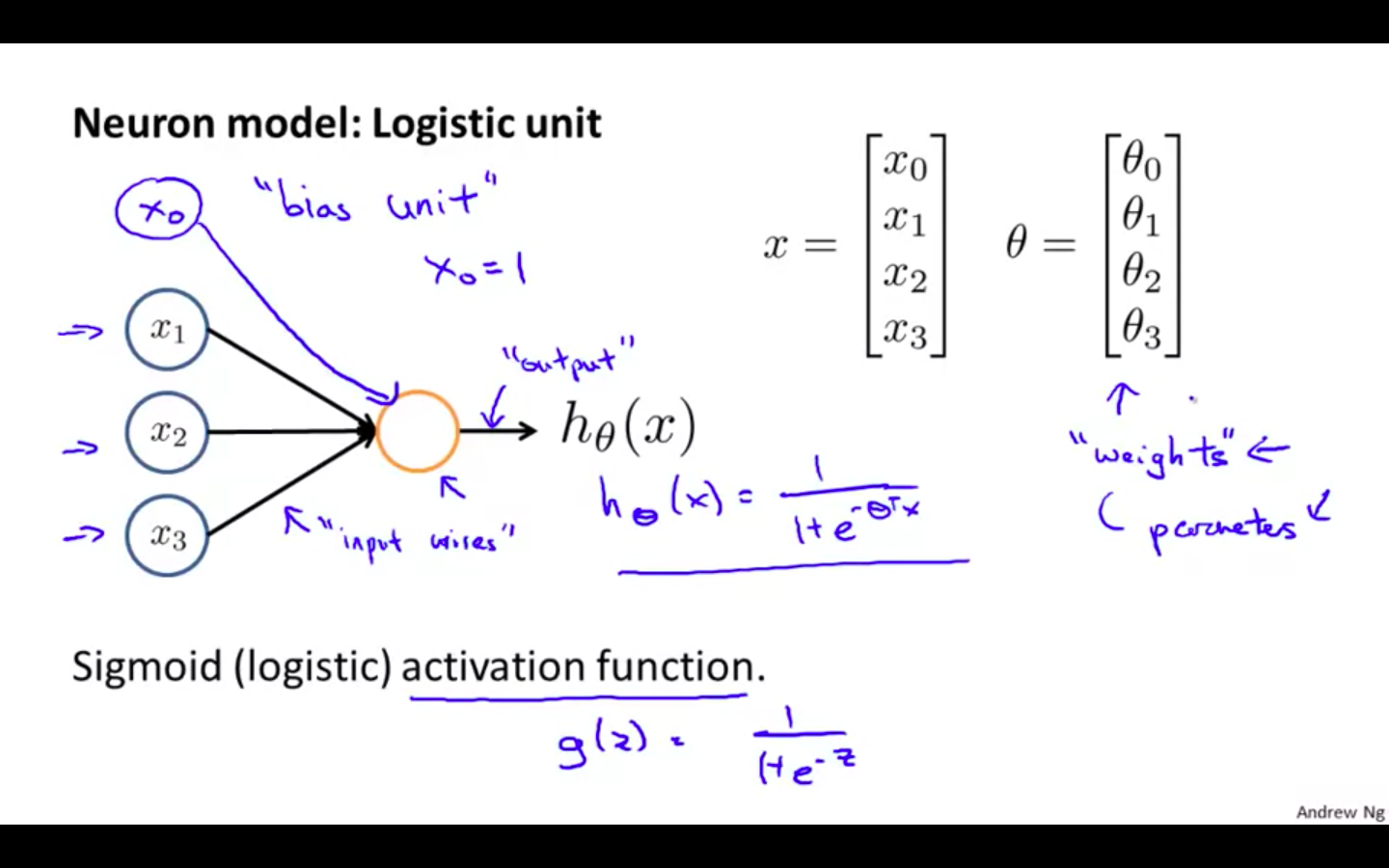
      • In our model, our dendrites are like the input features ( x_1, …. x_n ) and the output is the result of our hypothesis function.

      • In this model our x_0 input node is sometimes called the “bias unit.” It is always equal to 1.

      • Parameters are also called as weights

      • x_0 is a bias unit

      • Sigmoid ( logistic ) activation function

        • activation function = Hypothesis of logistic

      Neuron Model.png

  • Artificial Neural Network

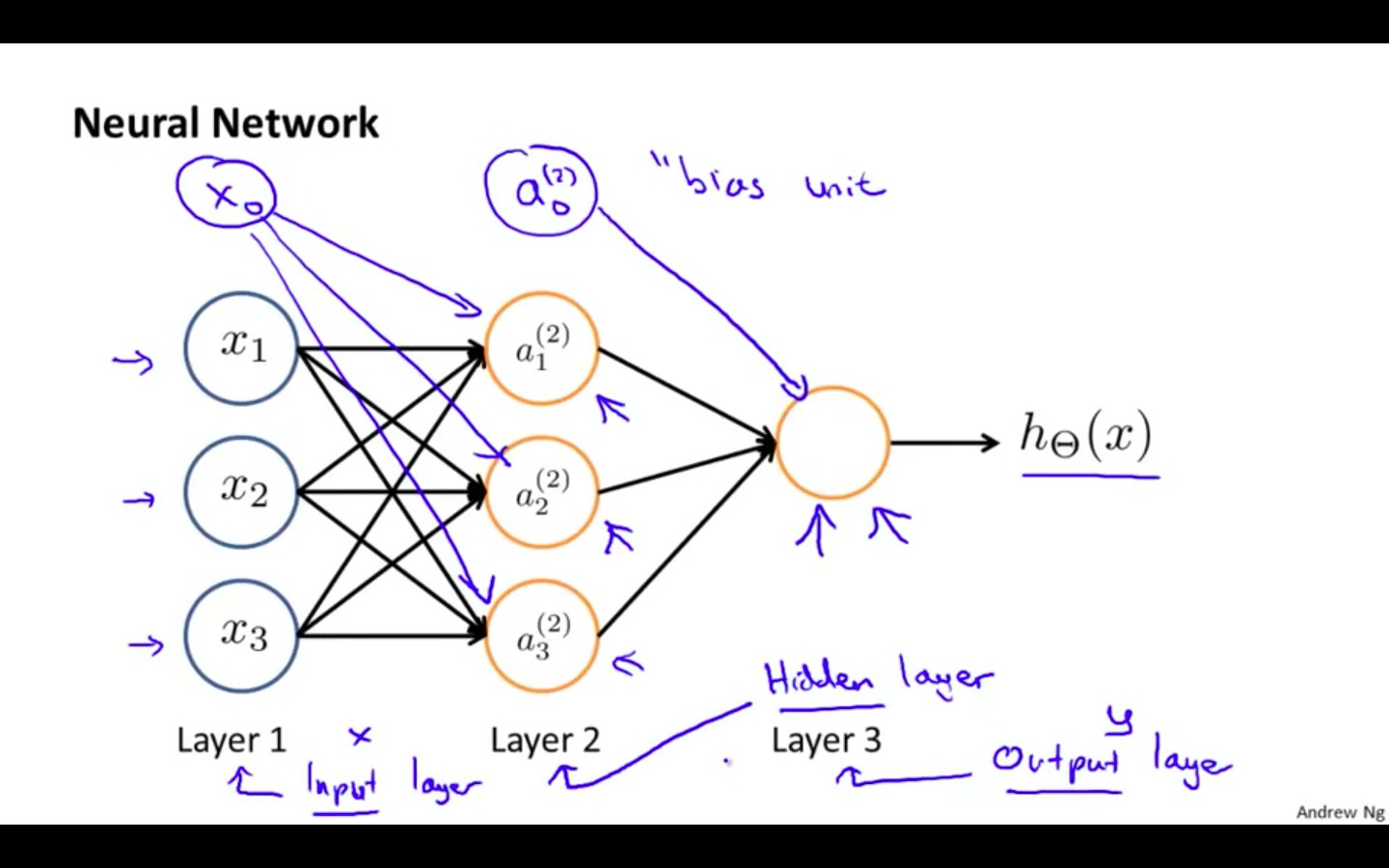
    • First layer is called as the input layer ( x )

    • Last layer is called as the output layer ( y )

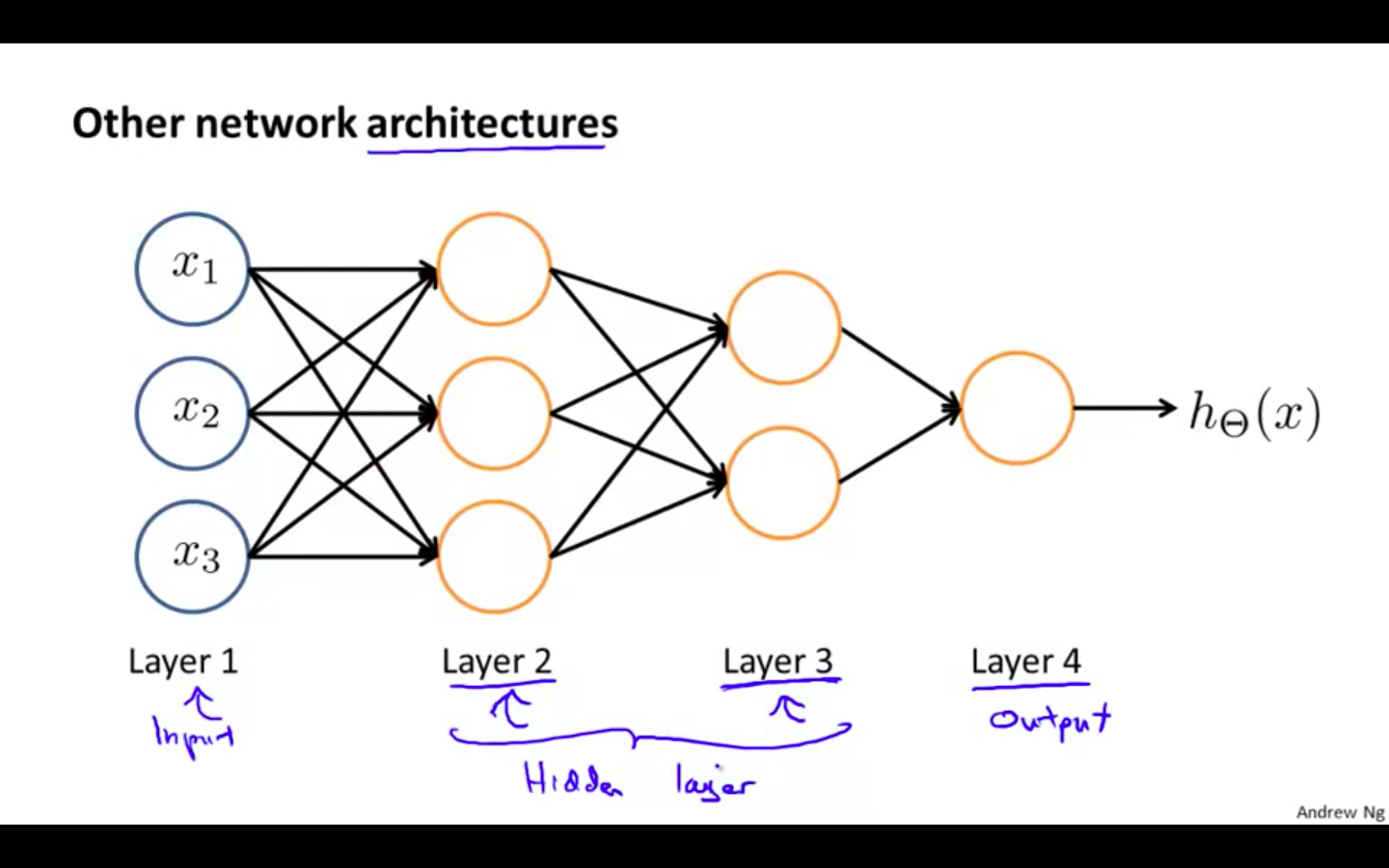
    • Layer between the first and the last layer is called as the hidden layer

    • First unit of the layer is called the bias unit

    Neural Network.png

    • a_i^j = “activation” of unit i in layer j

    • theta^j = matrix of weight controlling function mapping from layer j to layer j + 1

    • If network has s^j unit in layer j, s^j+1 units in layer j + 1, then theta^j will be of dimension s_j+1 x (s_j + 1)

    • We apply each row of the parameters to our inputs to obtain the value for one activation node.

    • Our hypothesis output is the logistic function applied to the sum of the values of our activation nodes, which have been multiplied by yet another parameter matrix theta^2 containing the weights for our second layer of nodes.

    Neural Network 1.png

Model Representation 2

  • Forward Propagation

    • Activation flows from input layer to output layer

    • vectorised implementation of the above functions.

    • Notice that in this last step, between layer j and layer j+1, we are doing exactly the same thing as we did in logistic regression.

    • Adding all these intermediate layers in neural networks allows us to more elegantly produce interesting and more complex non-linear hypotheses.

    Forward Propagation.png

  • Neural Network learning it’s own features

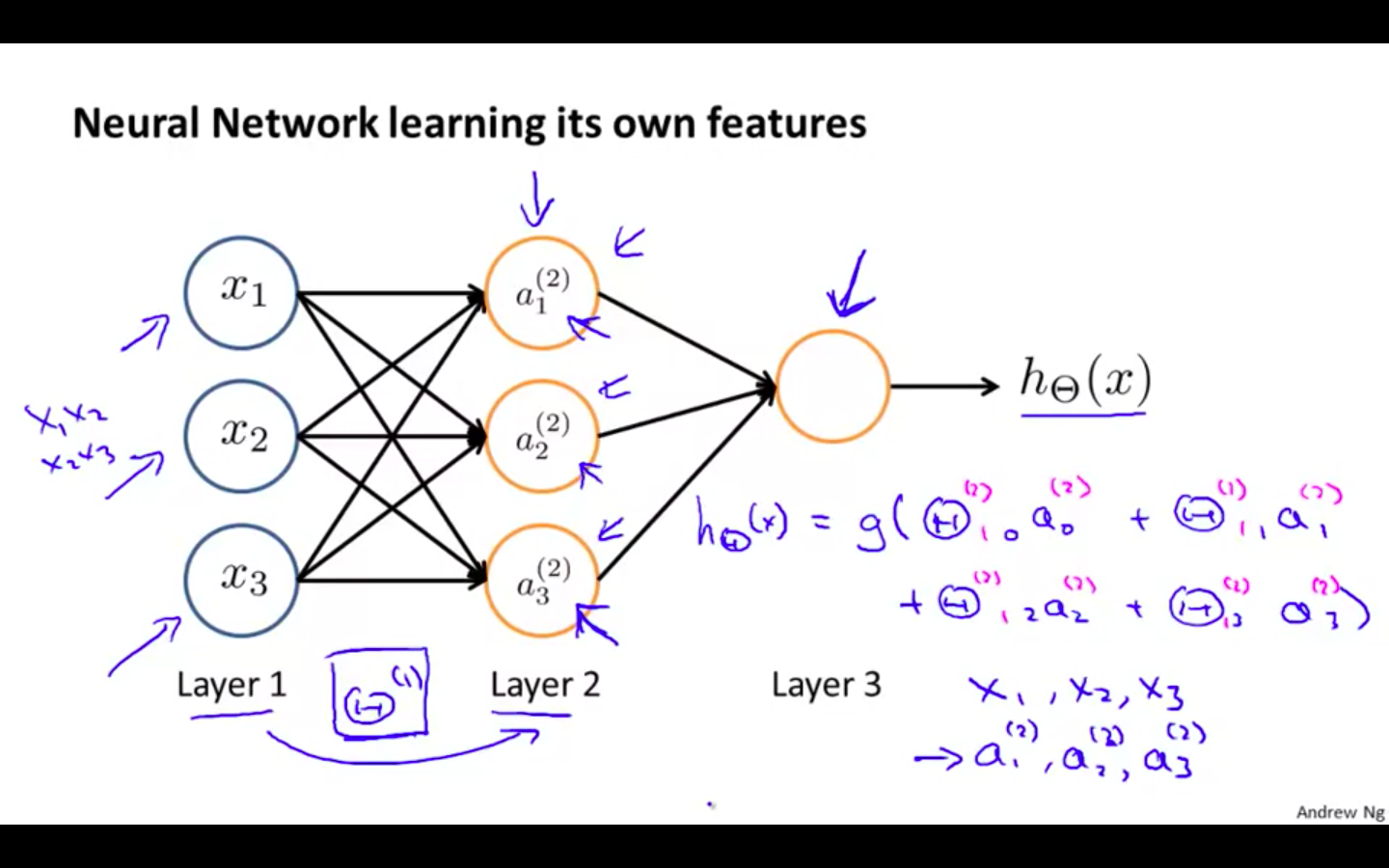
    NN Learning Features.png

  • Other Neural Network architectures

    NN Architectures.png

Applications

Examples and Intuitions 1

  • XOR / XNOR

    NN XOR:XNOR.png

  • AND

    • A simple example of applying neural networks is by predicting x_1 AND x_2, which is the logical ‘and’ operator and is only true if both x_1 and x_2 are 1

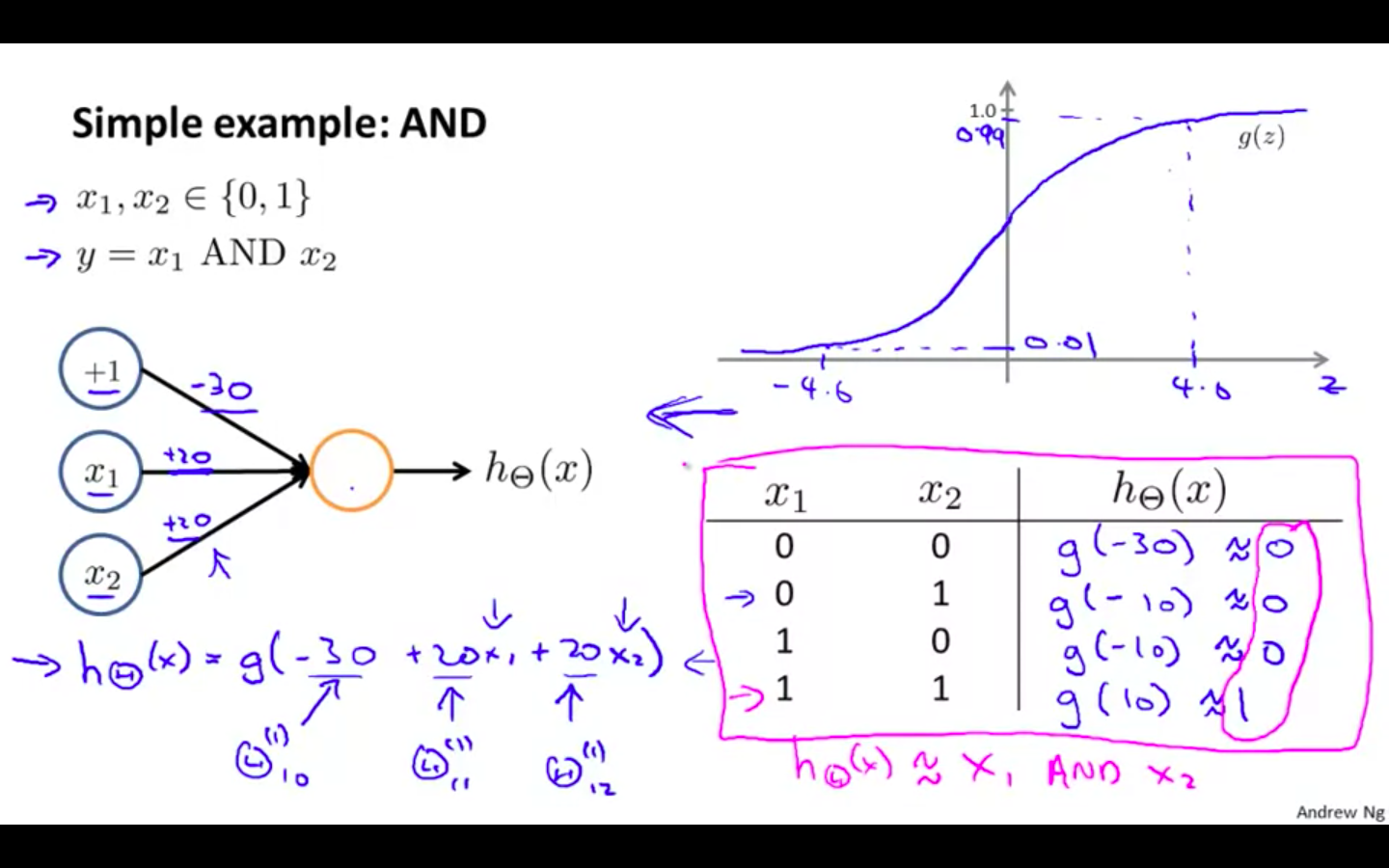
    NN AND.png

  • OR

    • Neural networks can also be used to simulate all the other logical gates.

    • The following is an example of the logical operator ‘OR’, meaning either x_1 is true or x_2 is true, or both

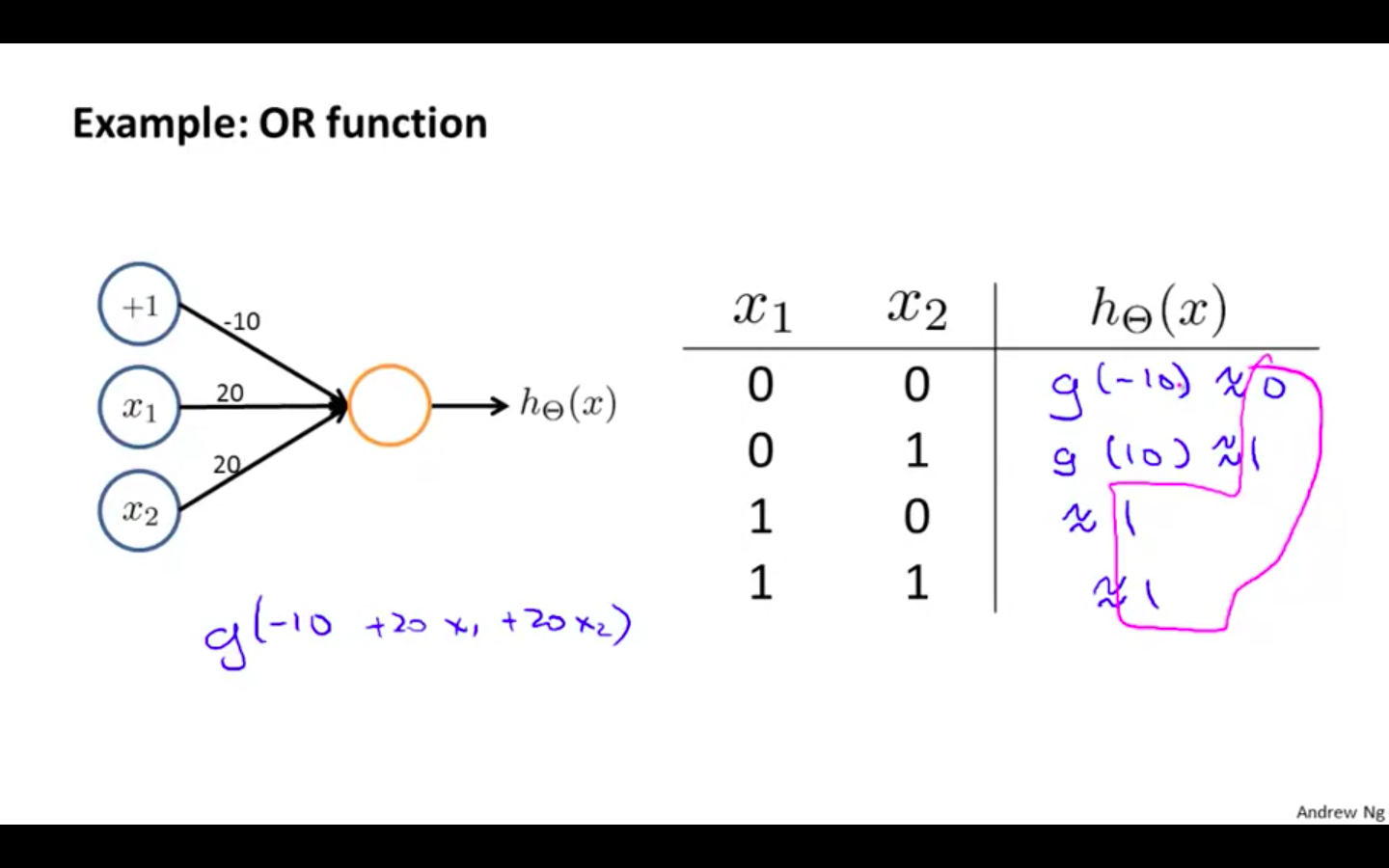
    NN OR.png

Examples and Intuitions 2

  • Negation

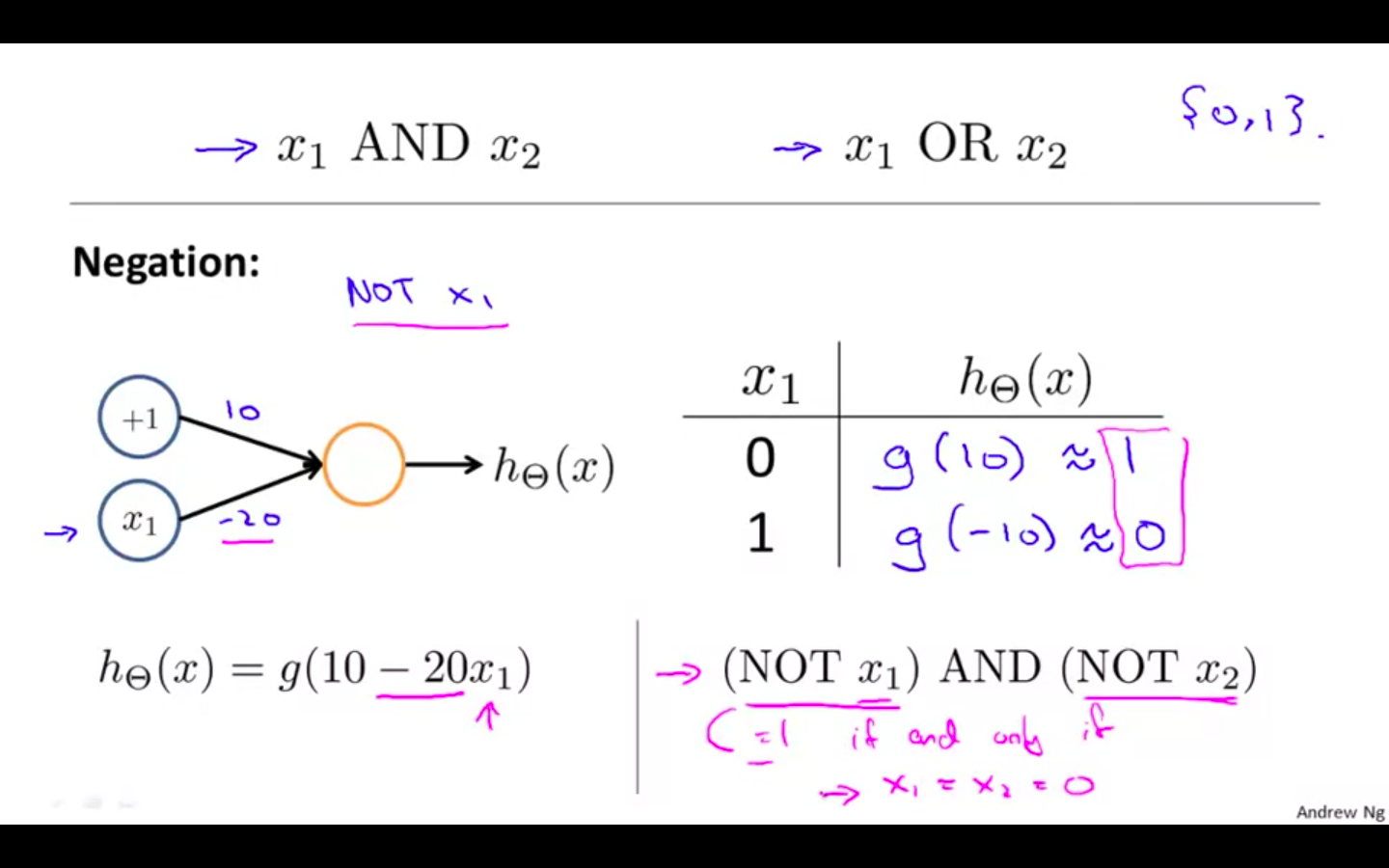
    NN Negation.png

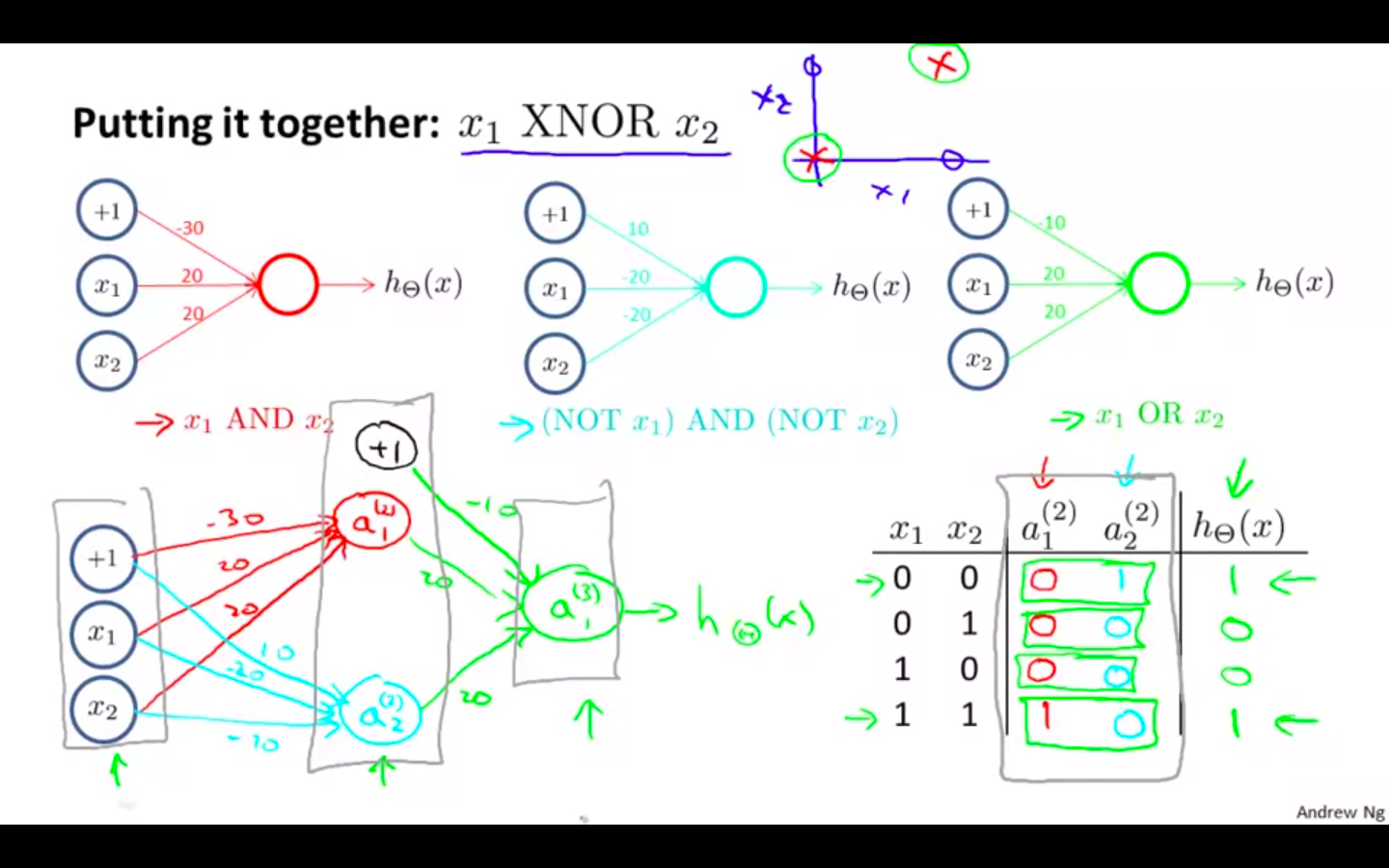
  • XNOR

    • Combining AND, NOT and OR function we have a XNOR operator

    NN XNOR.png

  • Intuition

    NN Intuition.png

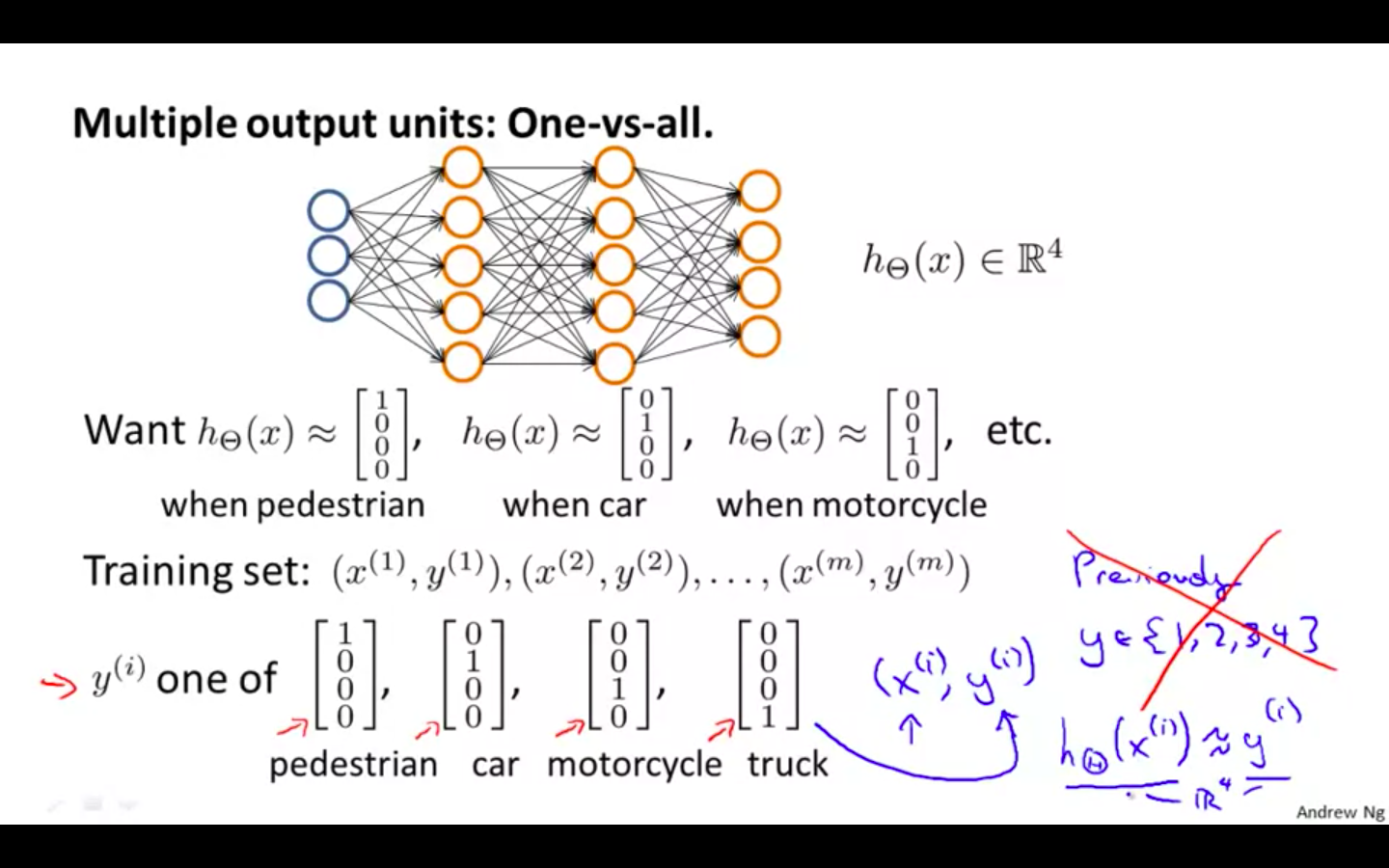
Multiclass Classification

  • One-vs-All

    • To classify data into multiple classes, we let our hypothesis function return a vector of values.

    • Say we wanted to classify our data into one of four categories. We will use the following example to see how this classification is done.

    • This algorithm takes as input an image and classifies it accordingly:

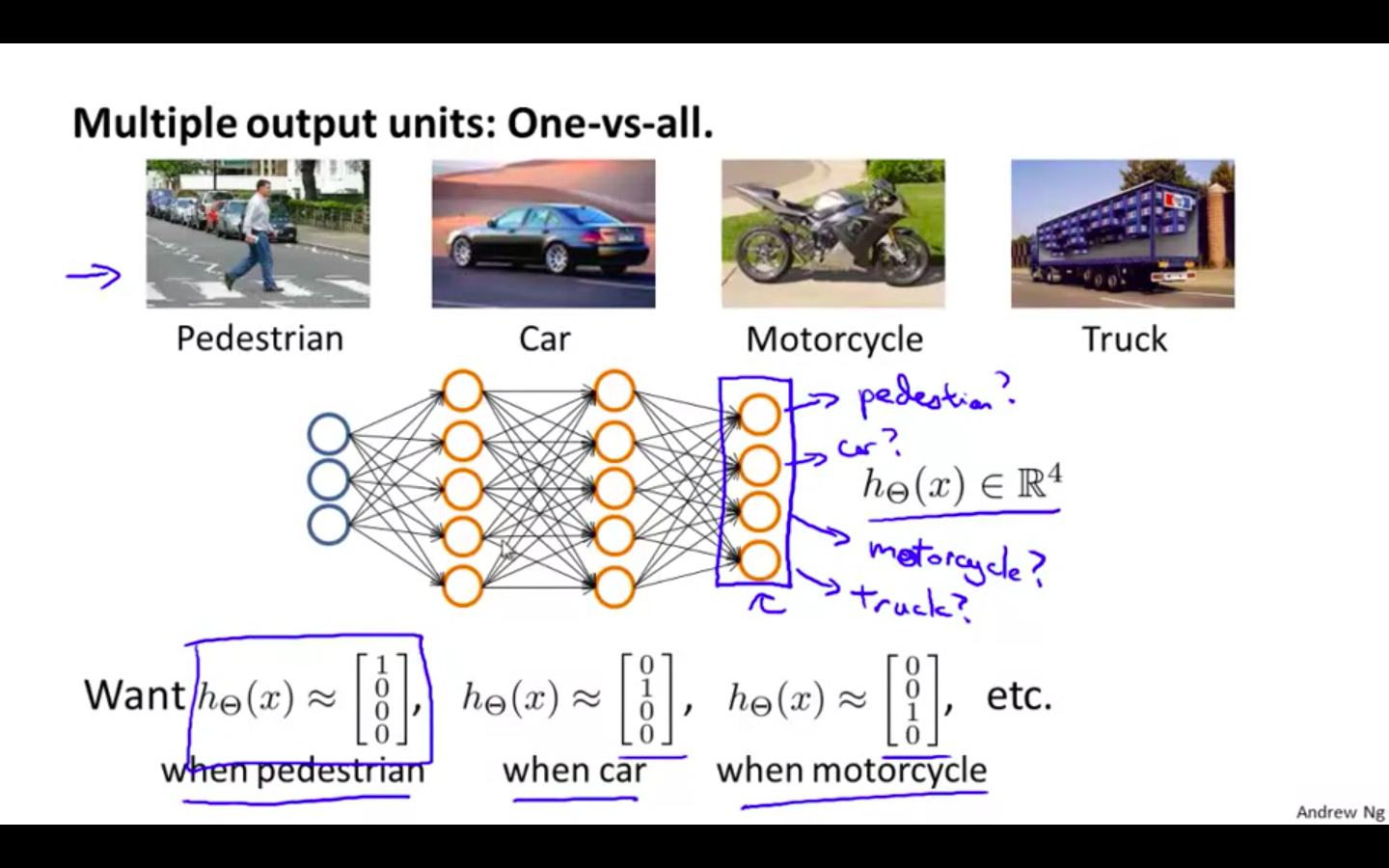
    NN OvsA.png

    • Our resulting hypothesis for one set of inputs may look like: hΘ​(x)=[0010​]

    NN OvsA 1.png