Clustering

Unsupervised Learning: Introduction

  • The data in the supervised learning problems comes with labels

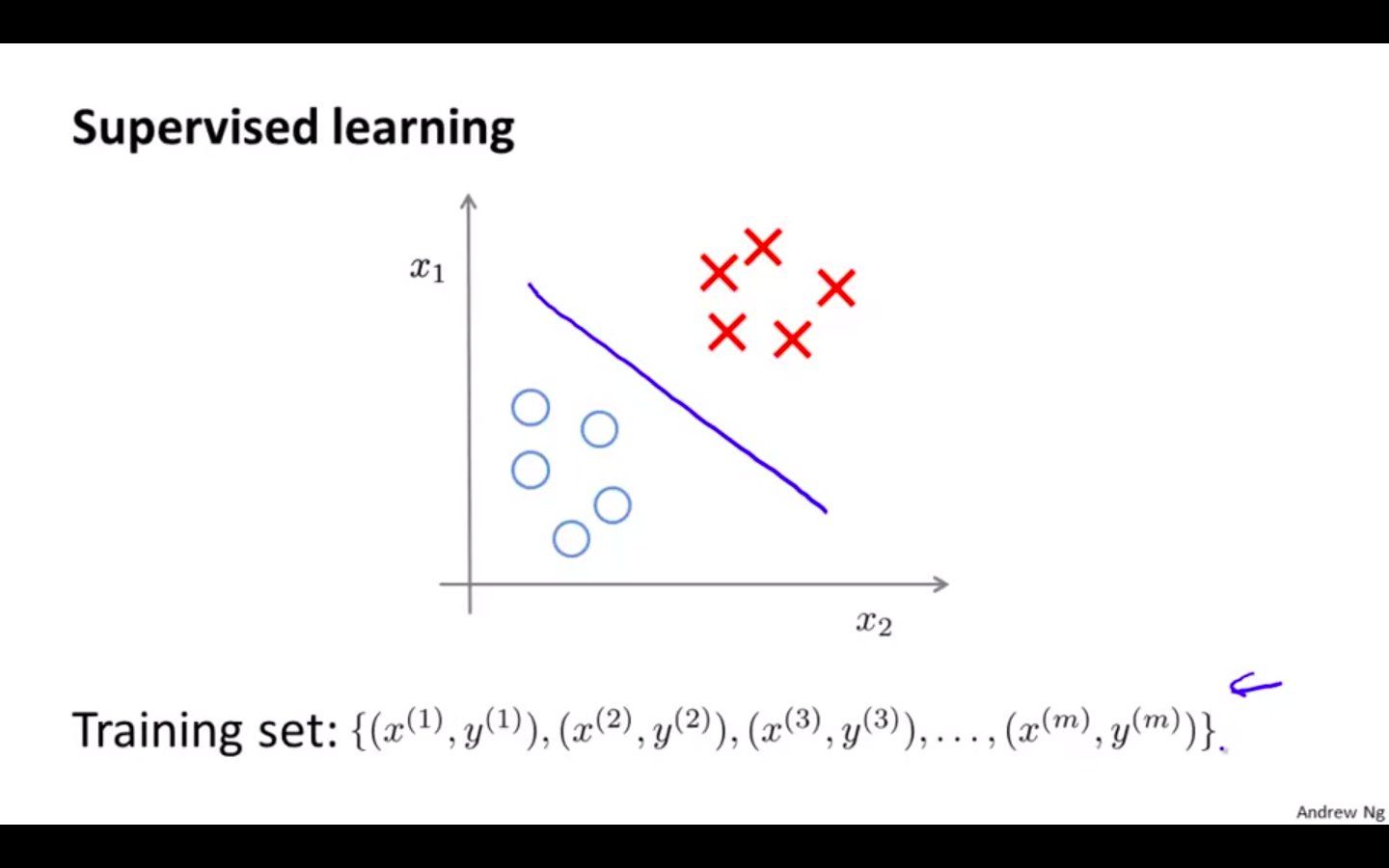
    Supervised Learning.png

  • The data in the unsupervised learning problems doesn’t come with the labels

  • Unsupervised learning algorithms are meant to find the structure in the dataset

  • Clustering algorithm is used find groups of data point on the dataset

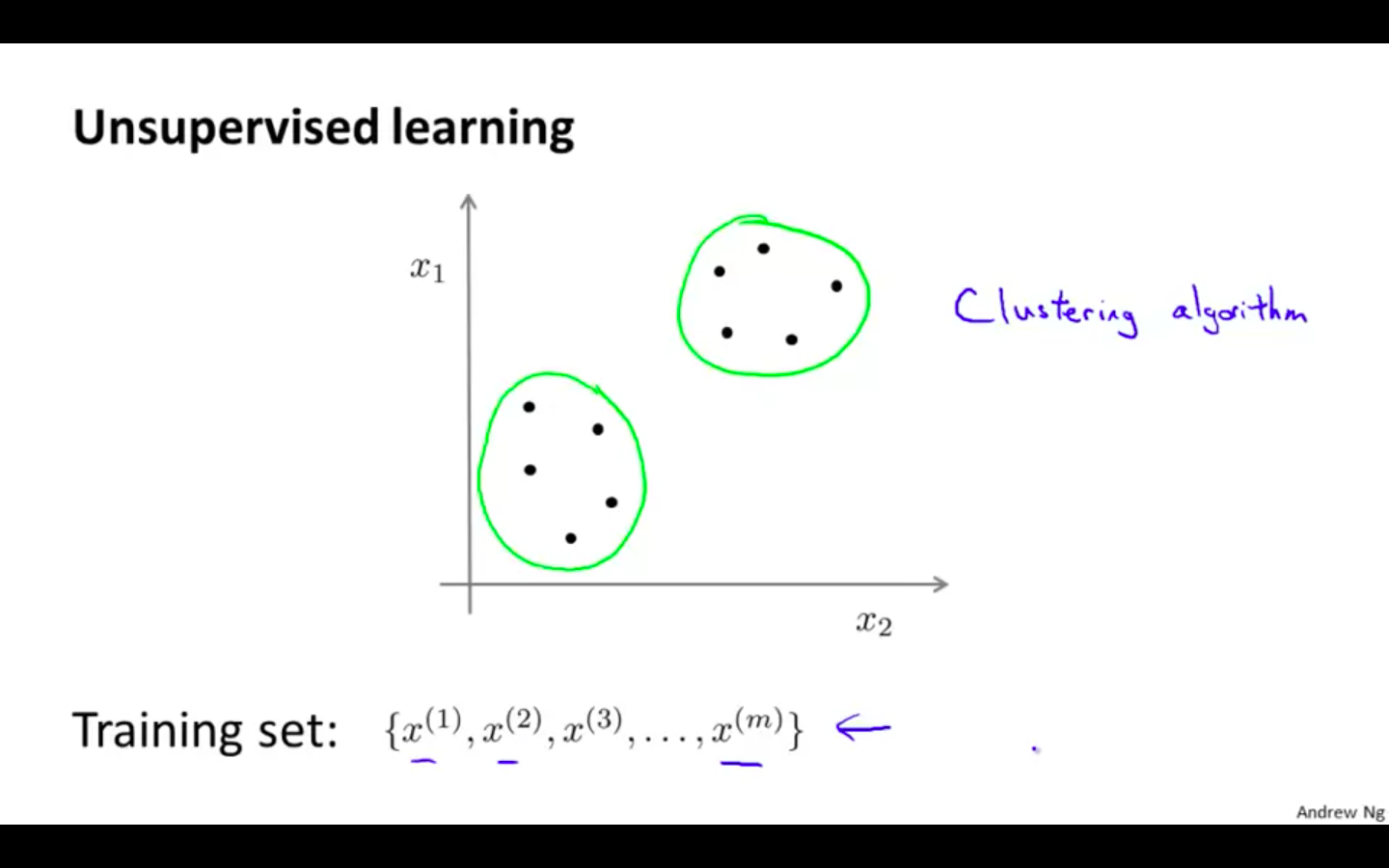
Unsupervised Learning.png

K-Means Algorithm

  • This is a Clustering Algorithm

  • Steps

    • Cluster Centroids

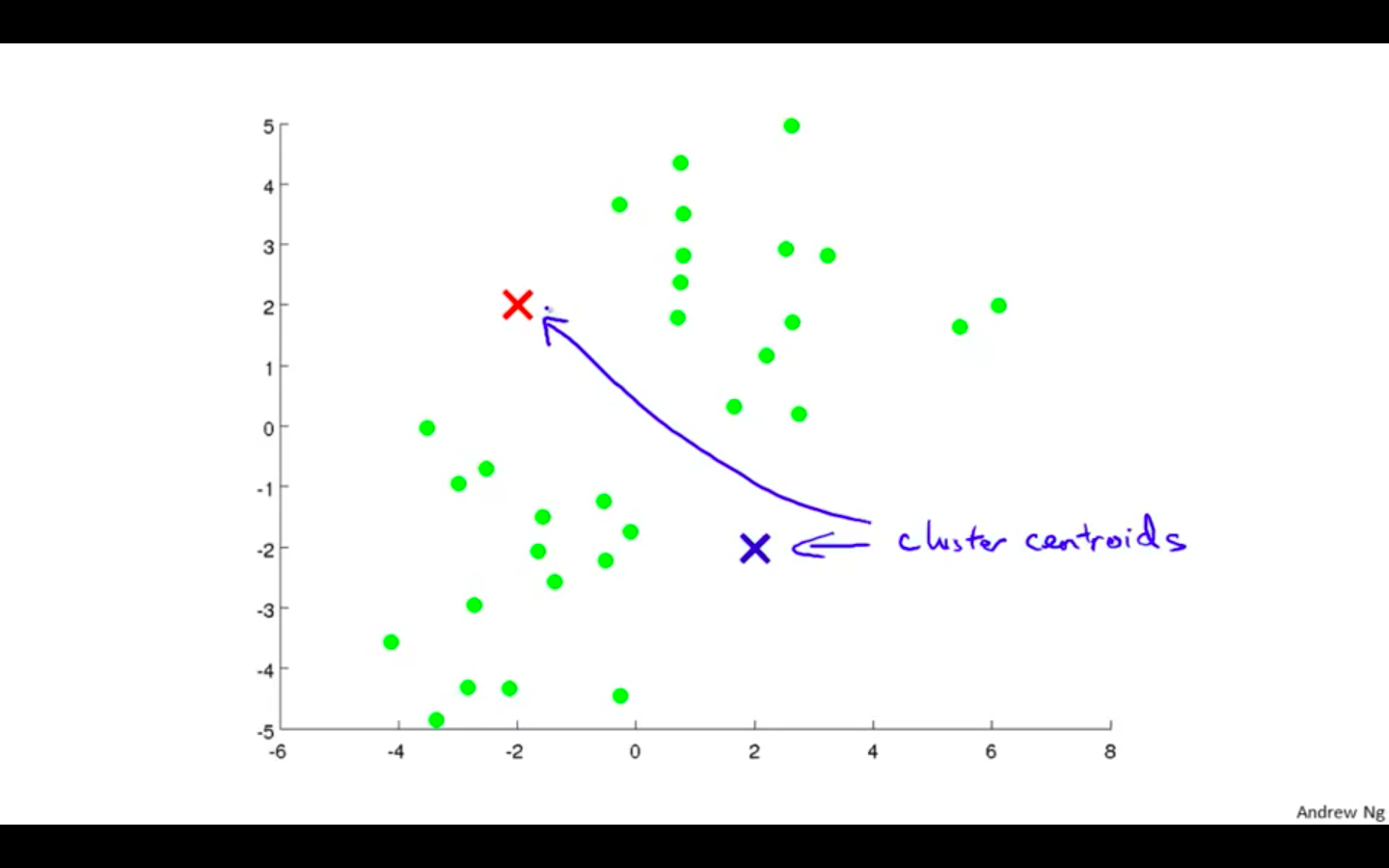
      Cluster Centroids.png

    • Random Initialisation

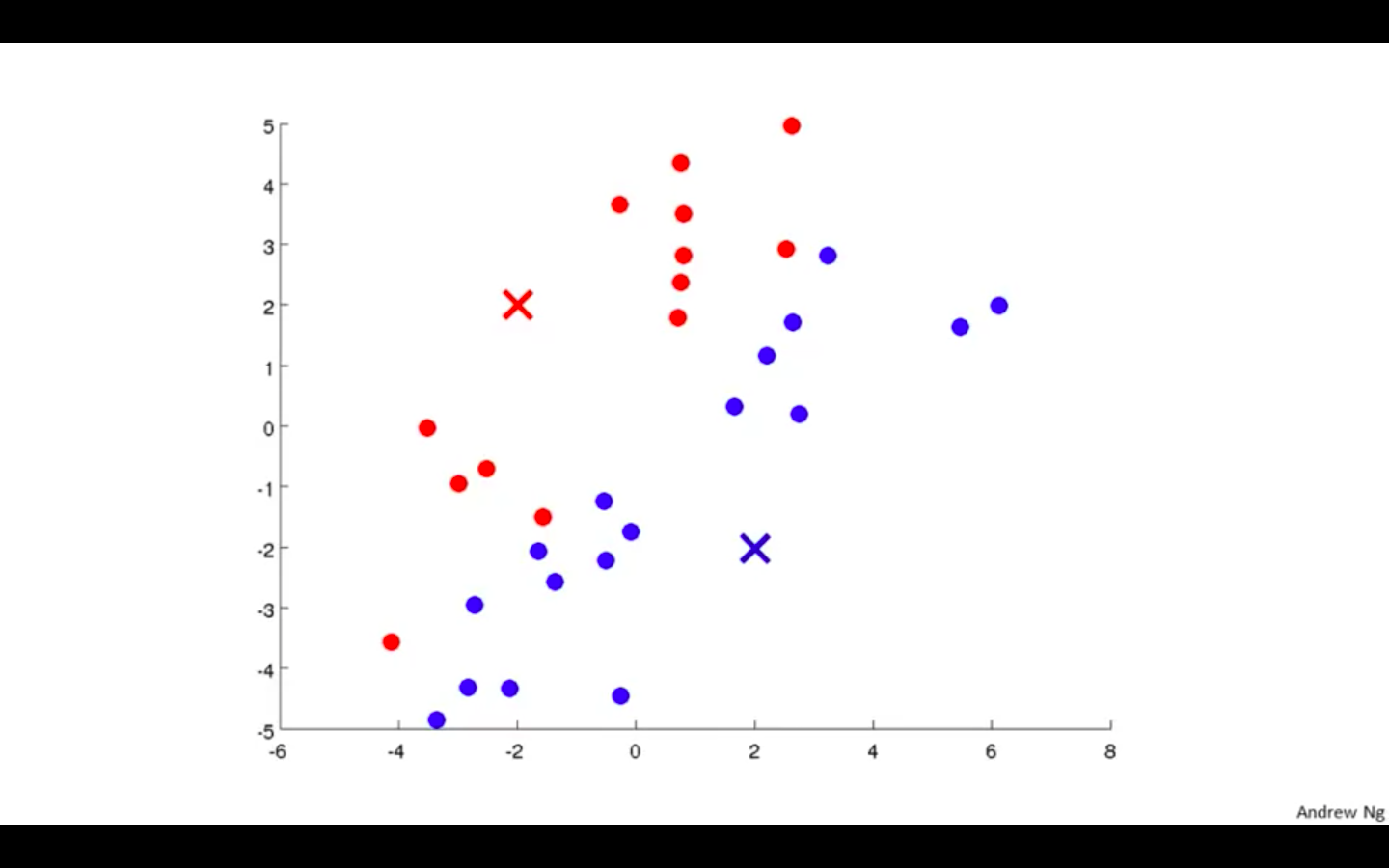
      Random Initialisation.png

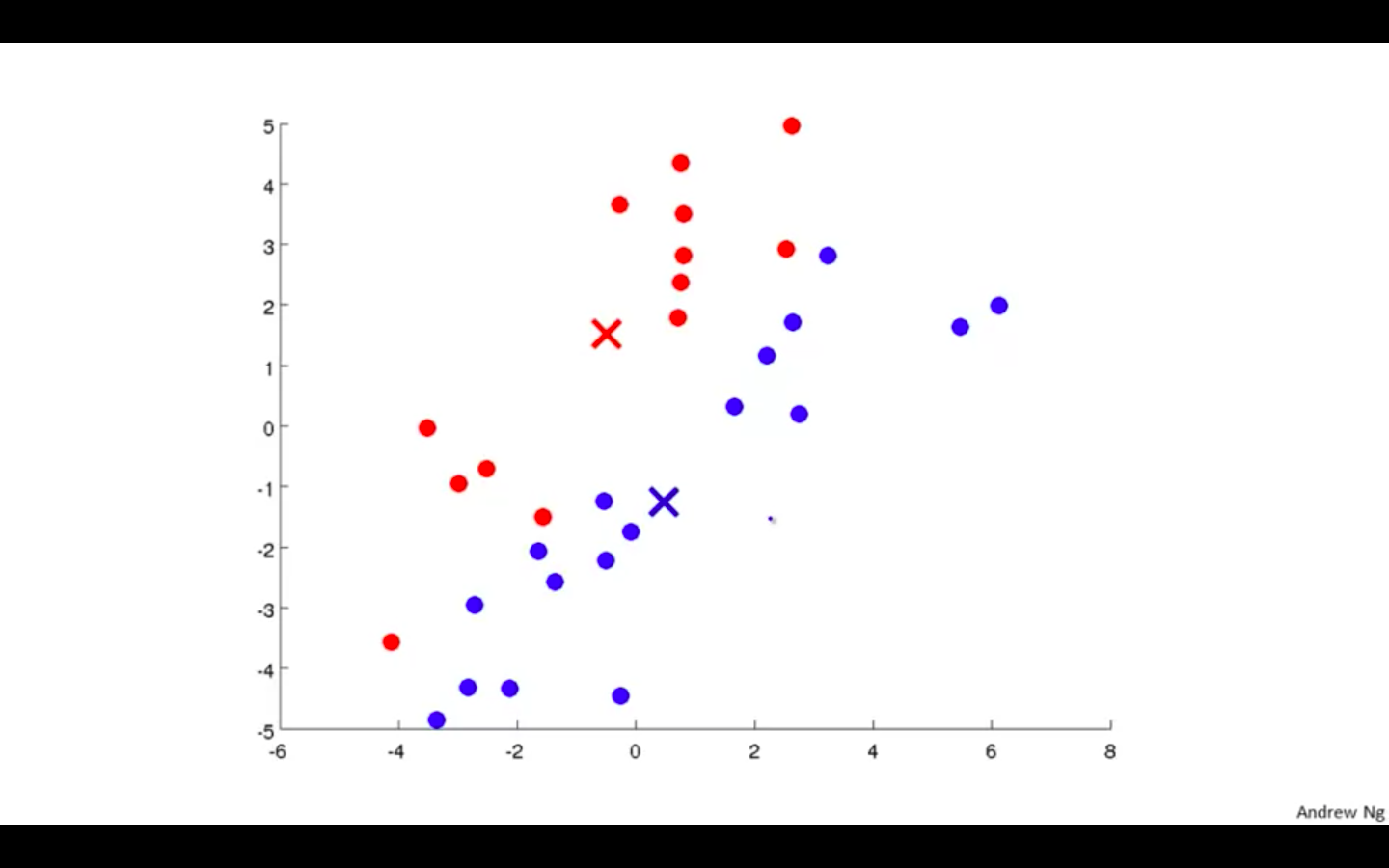
    • Mark a new cluster according to the points nearer to the centroids

    • Move Centroids to the average of new cluster

      Move To The Average.png

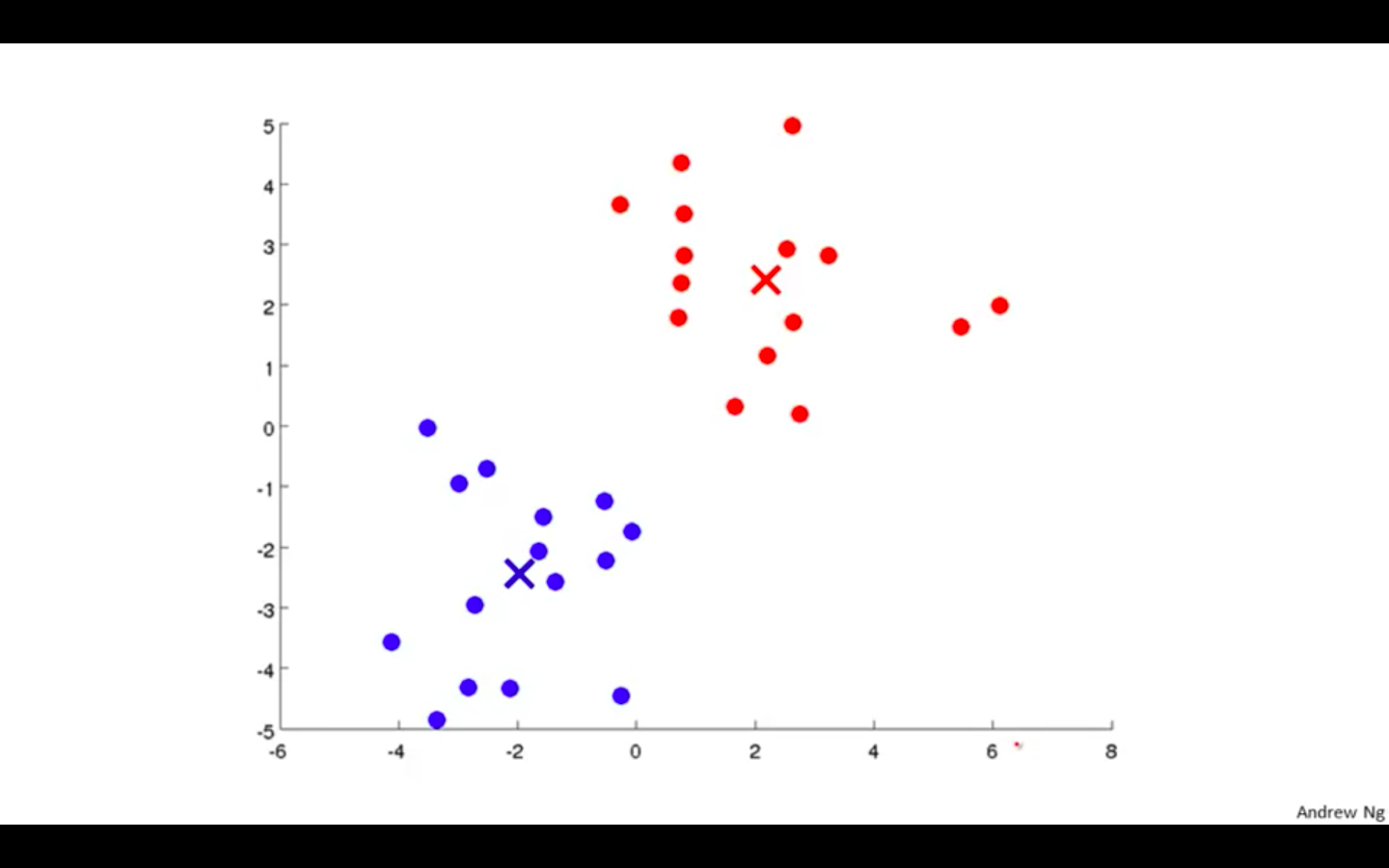
    • Repeat until the centroid doesn’t change

      Repeat.png

  • K-Means Algorithm

    • Input

      • K - number of clusters

      • Training Set

      K Means Algorithm.png

    • Overview Steps

      K Means Algorithm Extended.png

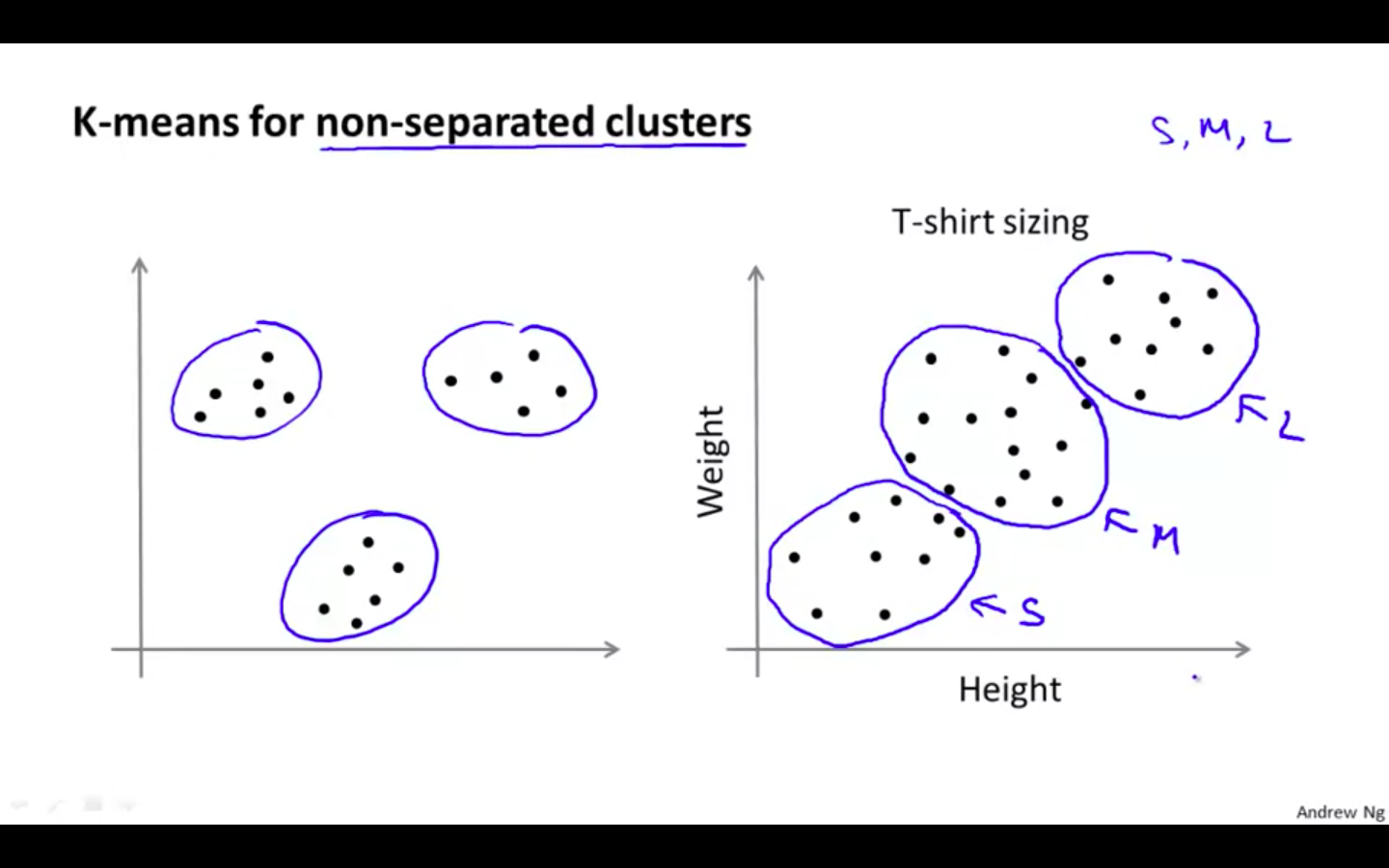
    • For Non-Separated Data

      Non Separated Clusters.png

Optimisation Objective

  • Optimisation Objective

    • Minimise the distance between the actual point and the centroid of the cluster associated

    Optimism Objective.png

  • Algorithm

    • First part of the algorithm consist of minimising cost function with respect to c^i holding u_k fixed

    • Second part of the algorithm consist of minimising cost function with respect to u_k

    Algorithm.png

Random Initialisation

  • Random Initialisation

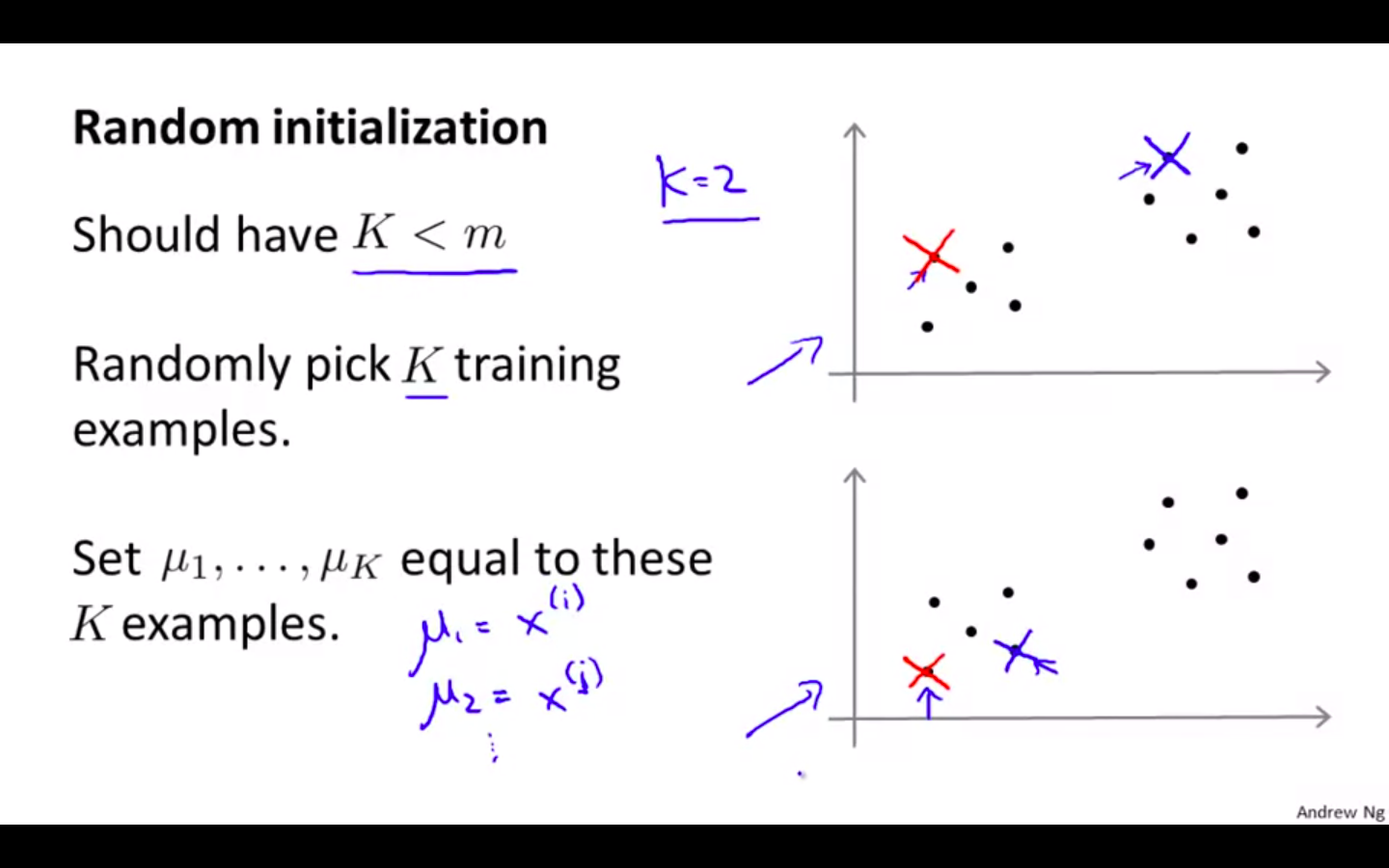
    • Should have K < m
    • Randomly pick K training examples
    • Set u_1….u_k to these K examples

    RI.png

  • Local Optima

    • K-Means can get stuck at local optima

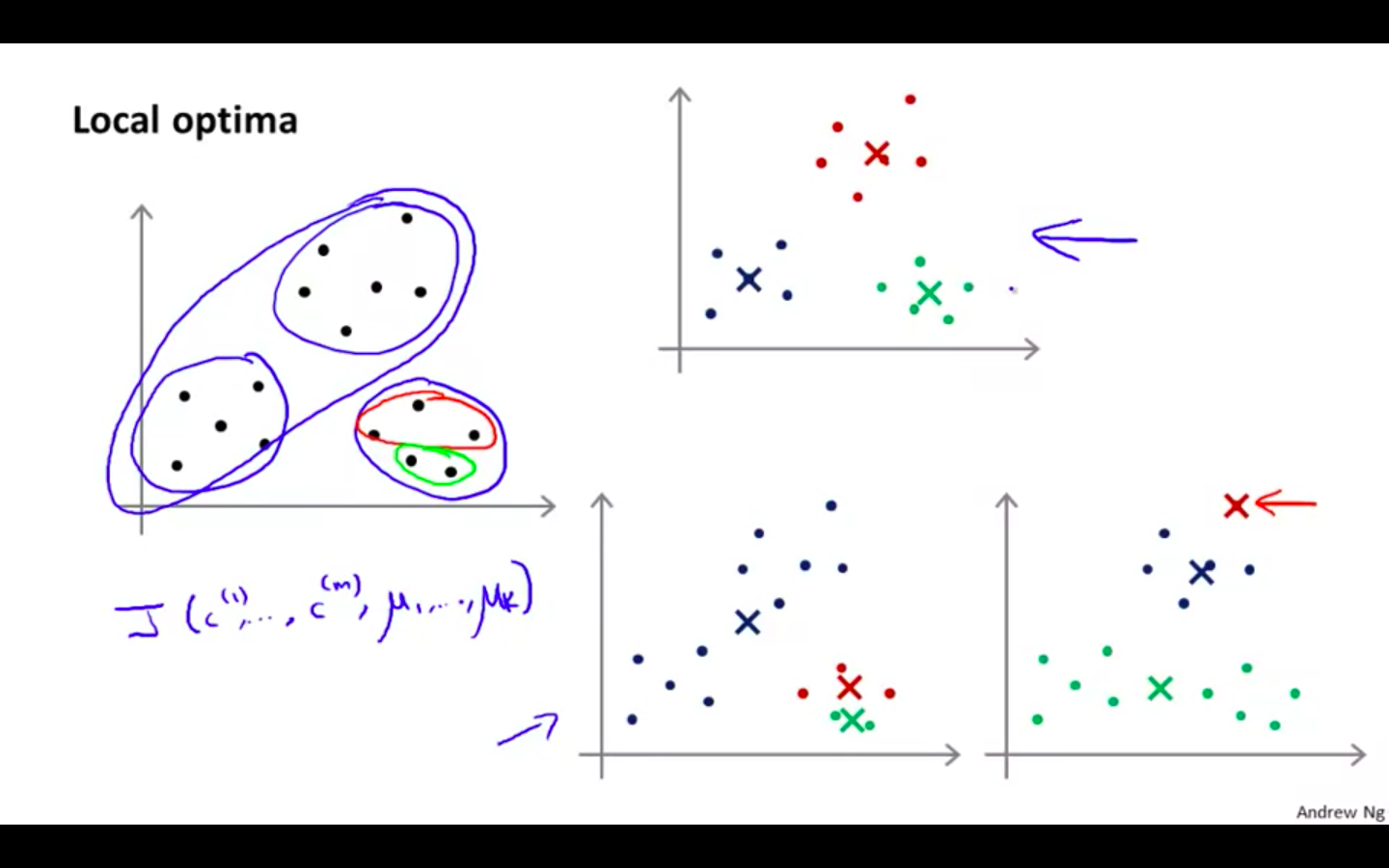
    Local Optima.png

  • Random Initialisation Extended

    • Run K-Means for n number of times

      • n = 50 to 1000

    • Pick the iteration which gives the minimum cost function

    RI Extended.png

Choosing the Number of Clusters

  • What is the right value of K ?

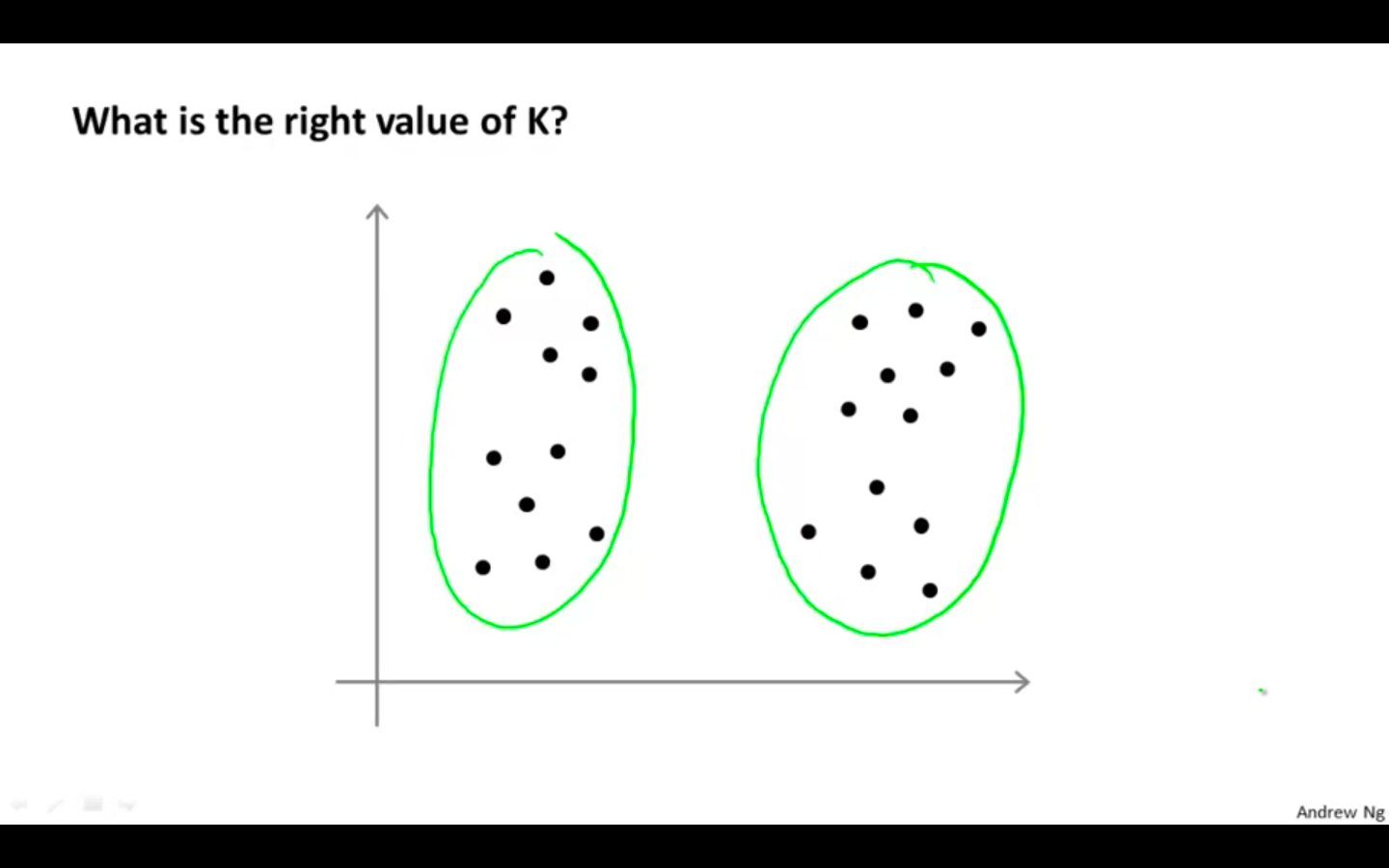
    Right value of k?.png

  • Elbow Method

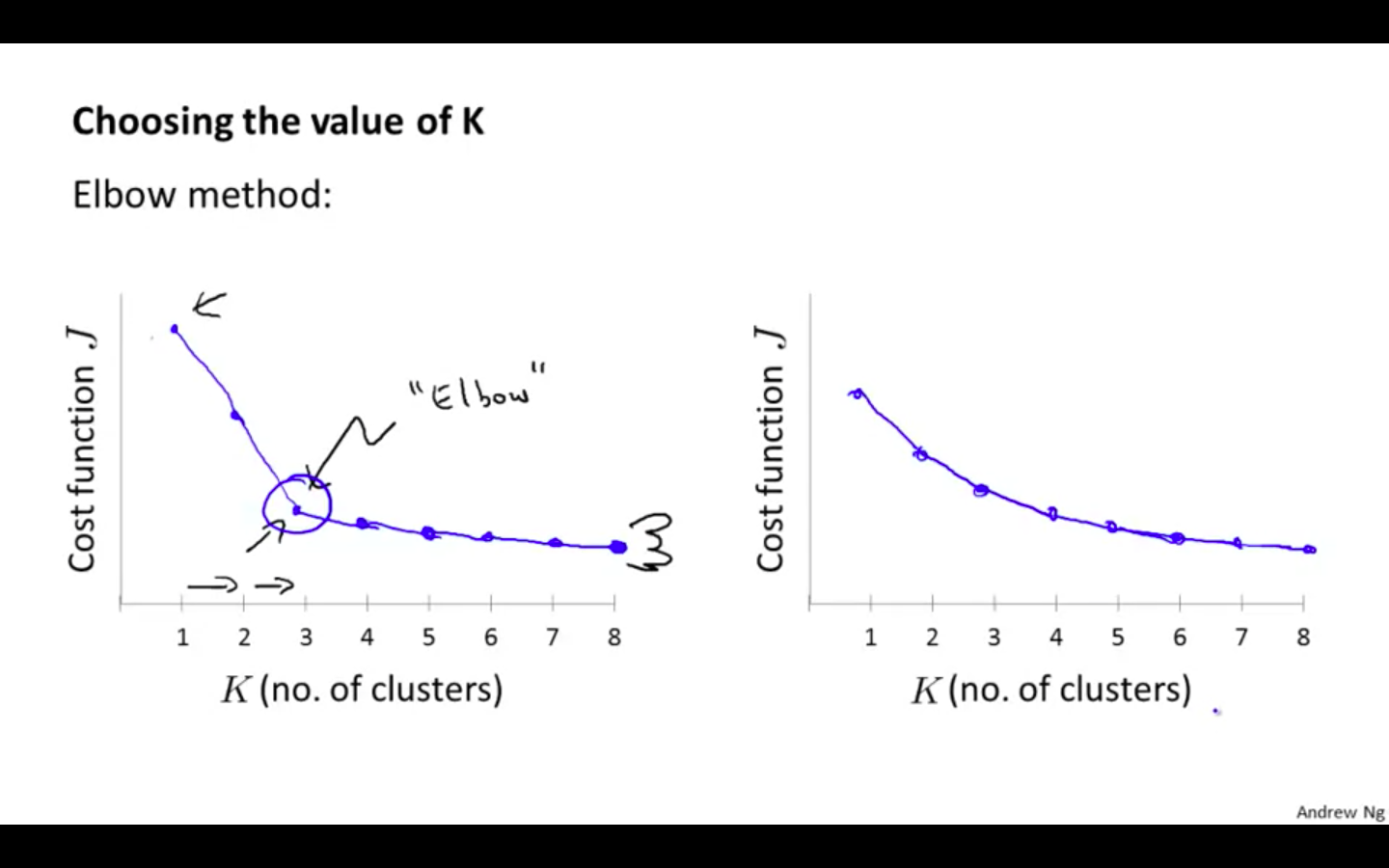
    Elbow Method.png

  • Other Method

    • Choosing the value of K based on the application

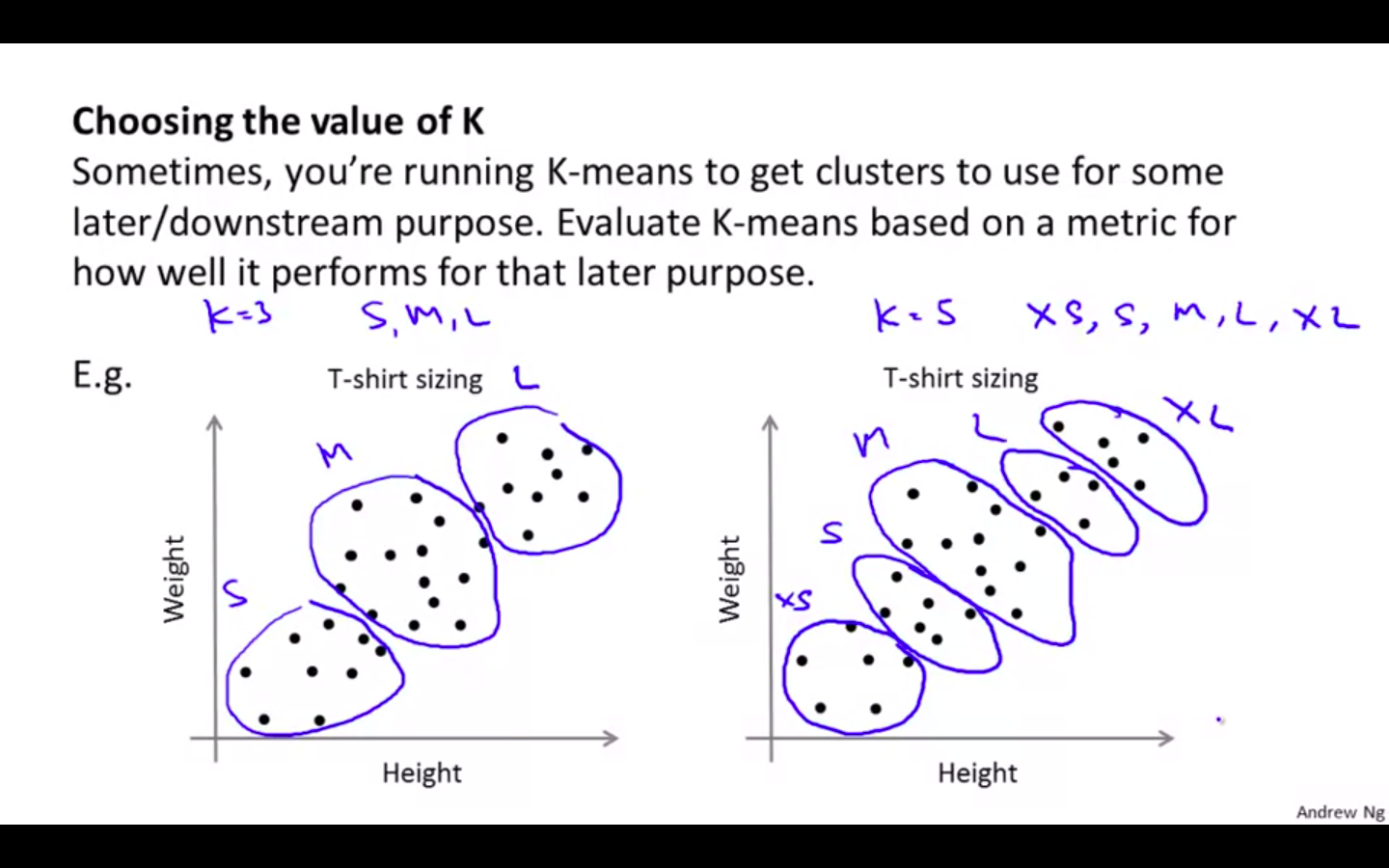
    Other Method.png

Motivation

Motivation 1: Data Compression

  • Data Compression

    • Compressing the size of the data

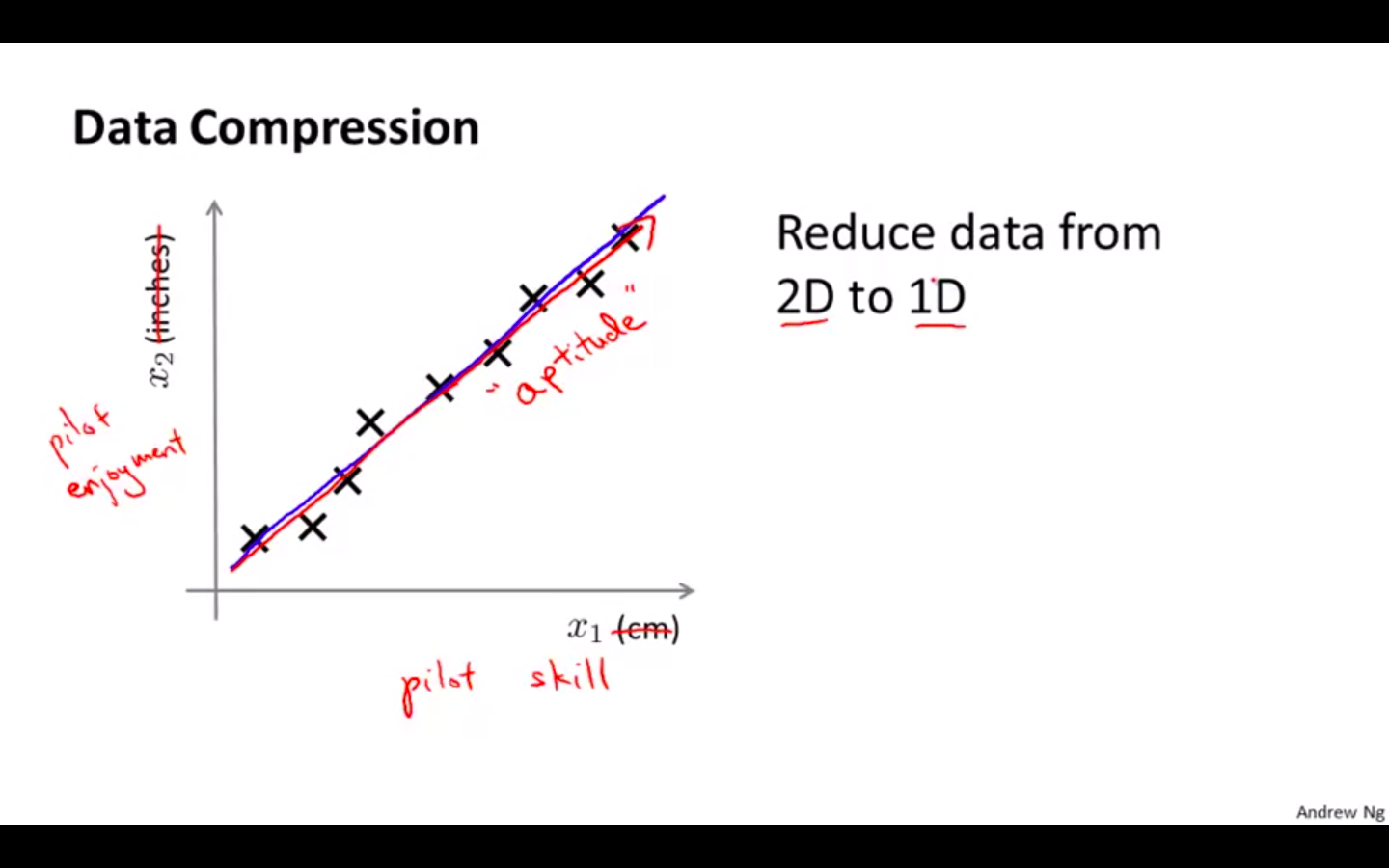
    Data Compression.png

  • 2D to 1D

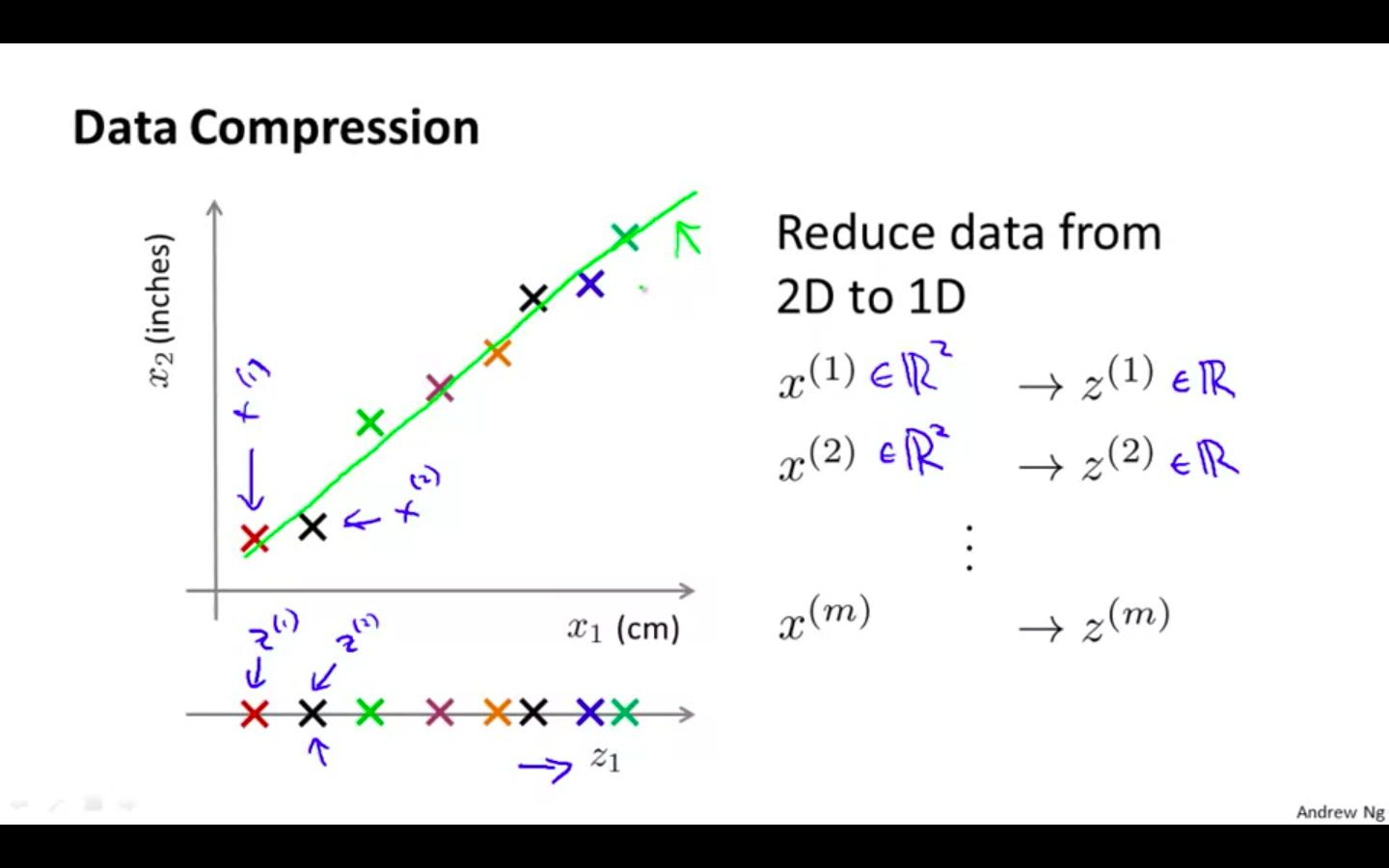
    2D - 1D.png

  • 3D to 2D

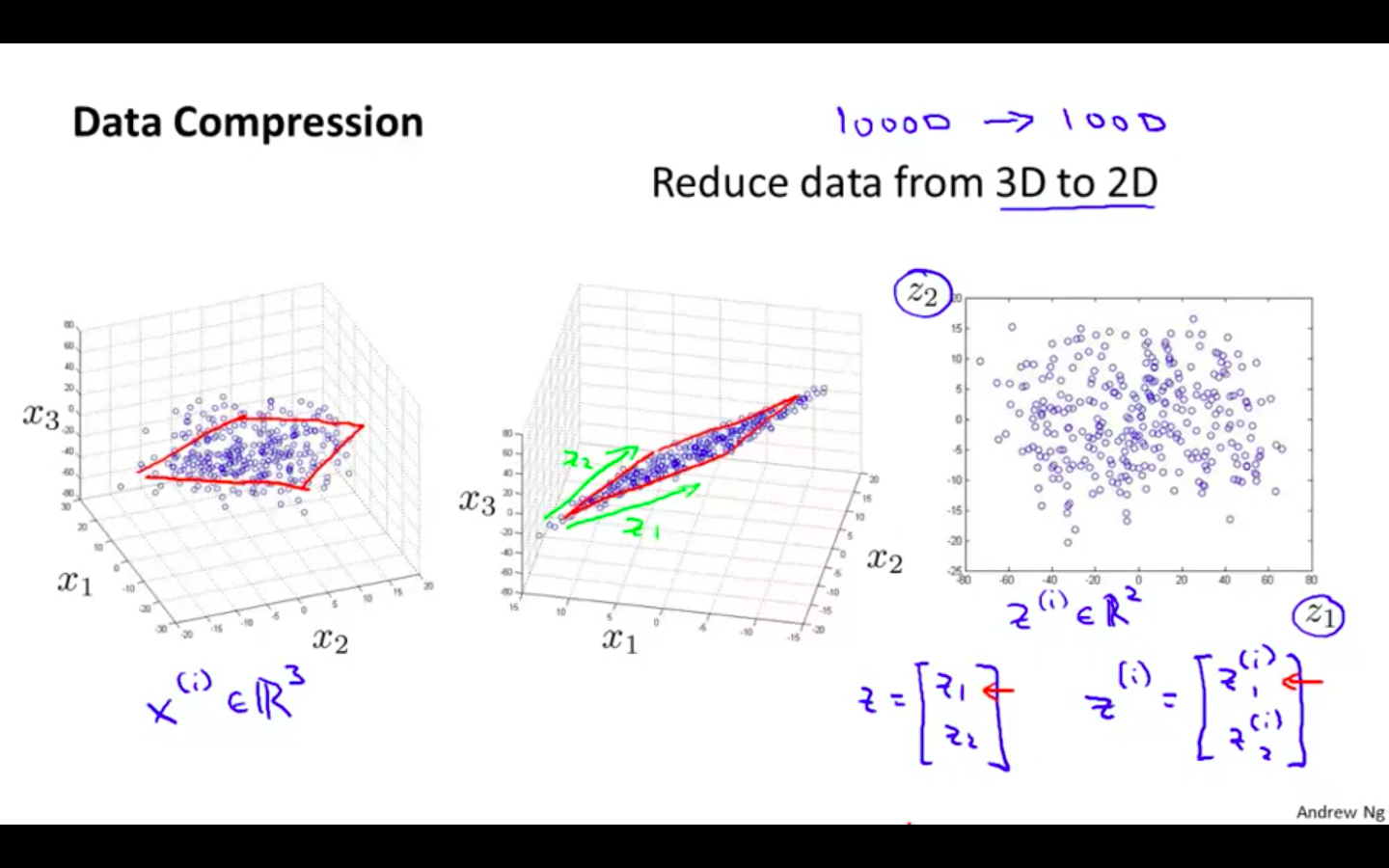
    3D - 2D.png

Motivation 2: Visualisation

  • Data Visualisation

    • Dataset of countries with many features

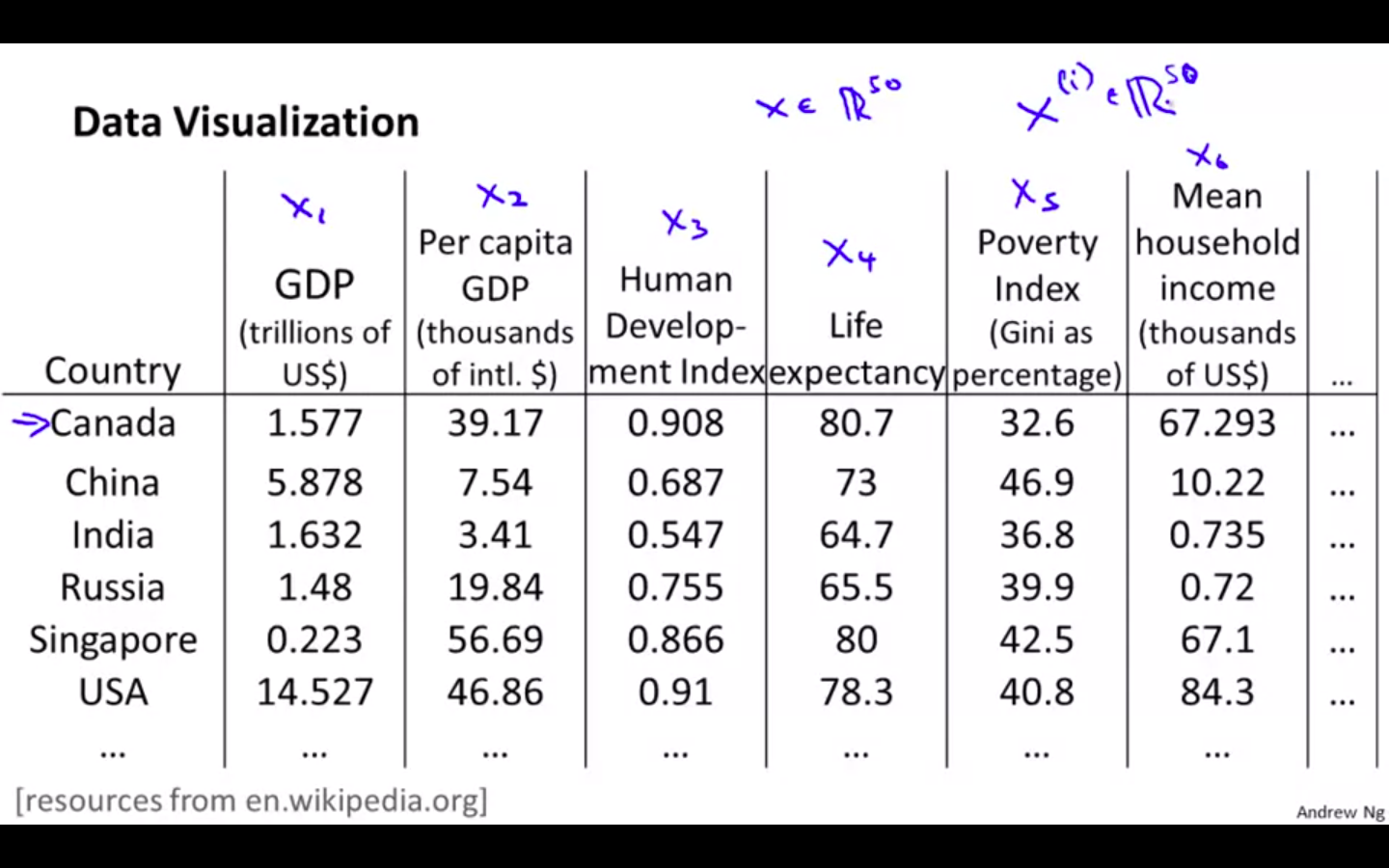
    Data Visualisation 1.png

    • Converting 50 D to 2 D

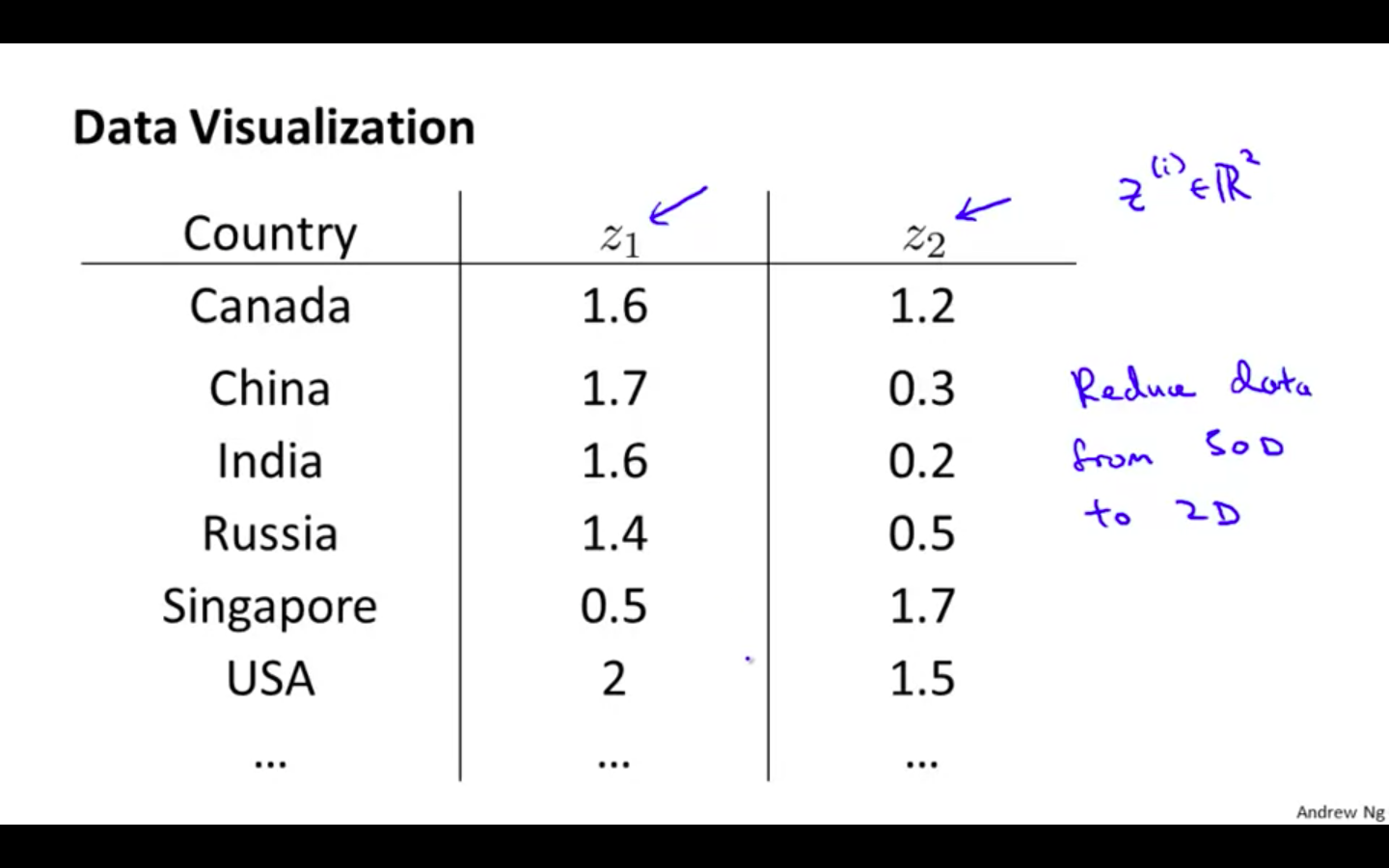
    Data Visualisation 2.png

    • Plotting the dataset

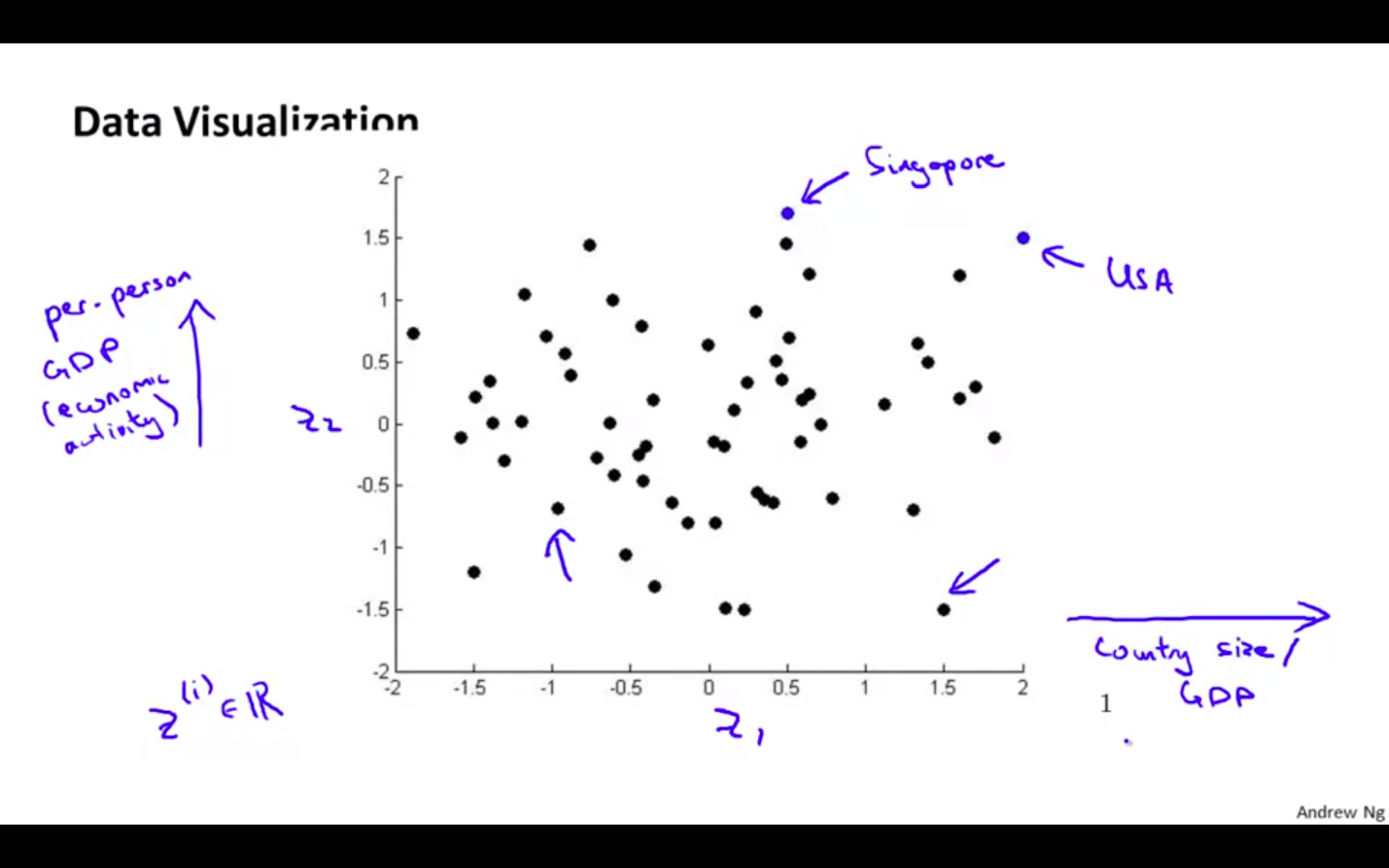
    Data Visualisation 3.png

Principal Component Analysis

Principal Component Analysis Problem Formulation

  • PCA

    • Dimension Reductionality Algorithm

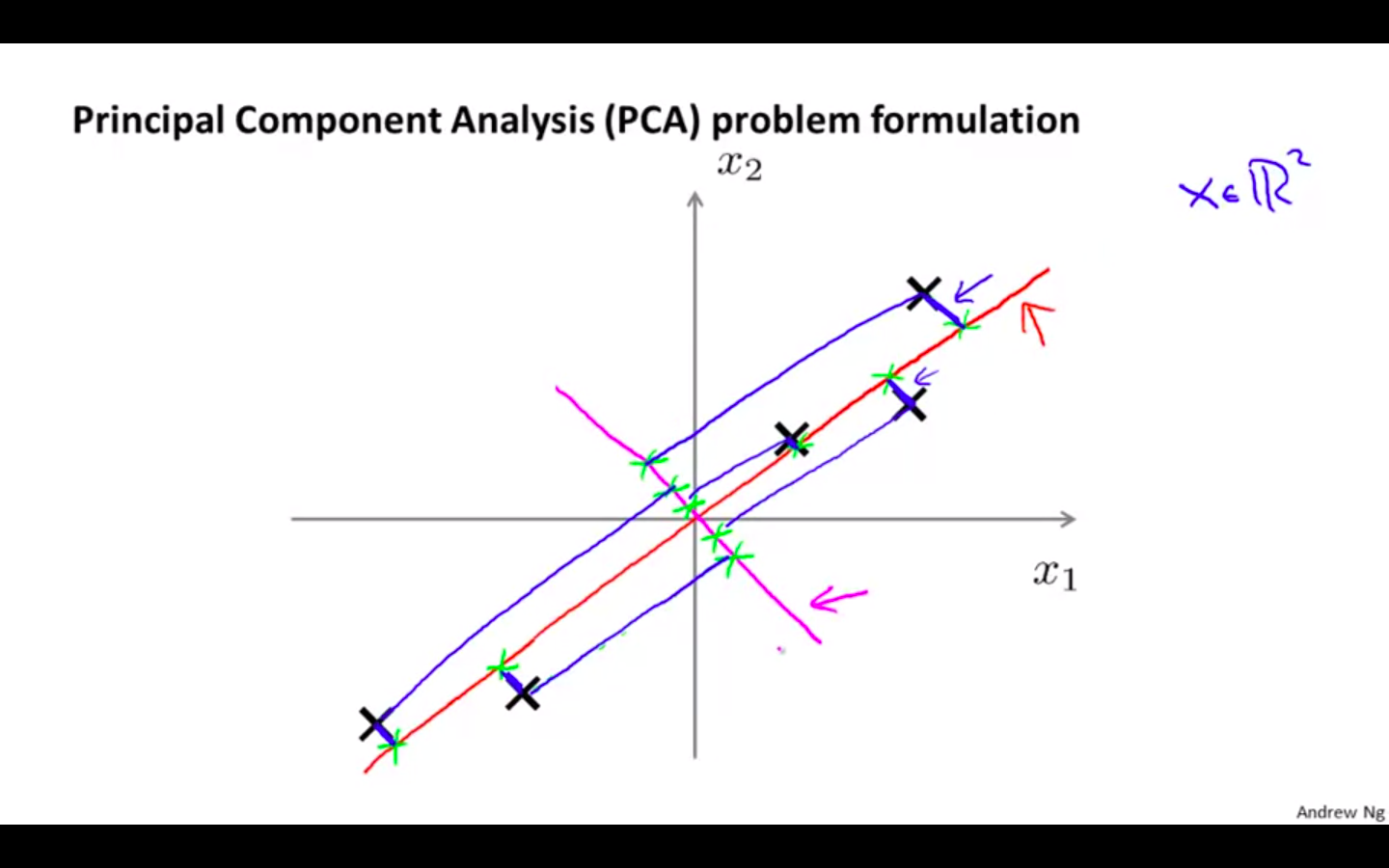
    PCA.png

    • Problem Formulation

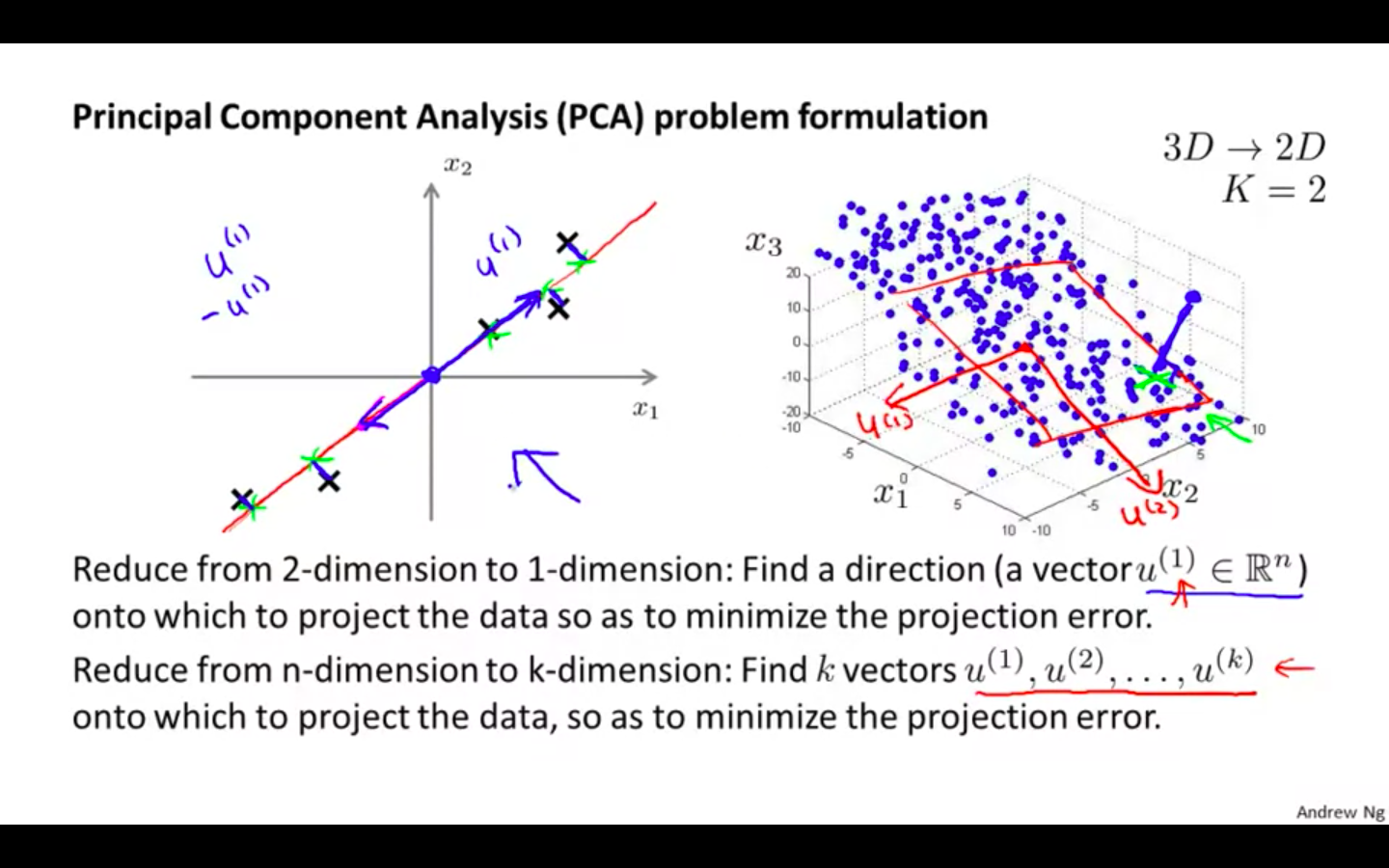
    PCA Problem Formulation.png

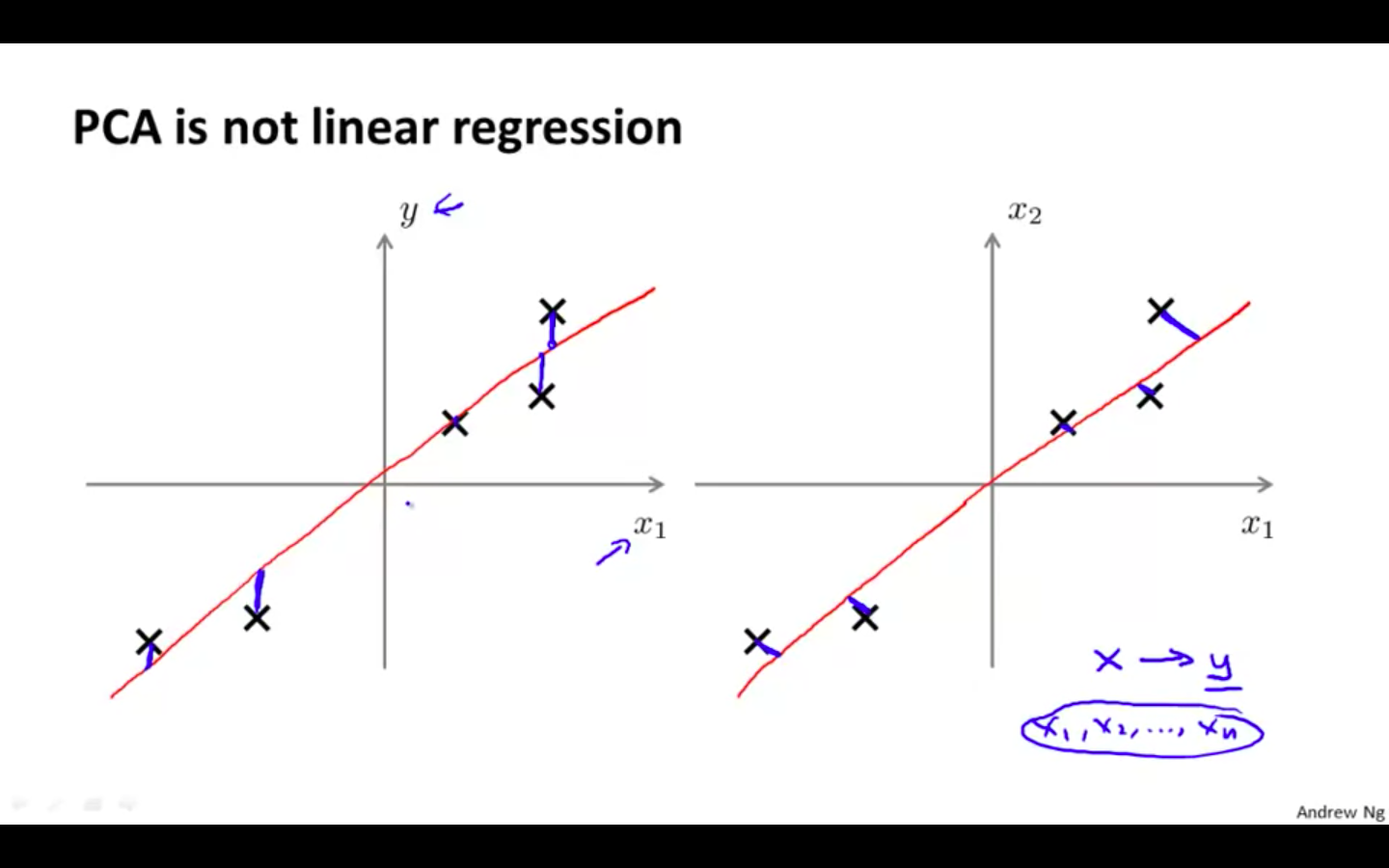
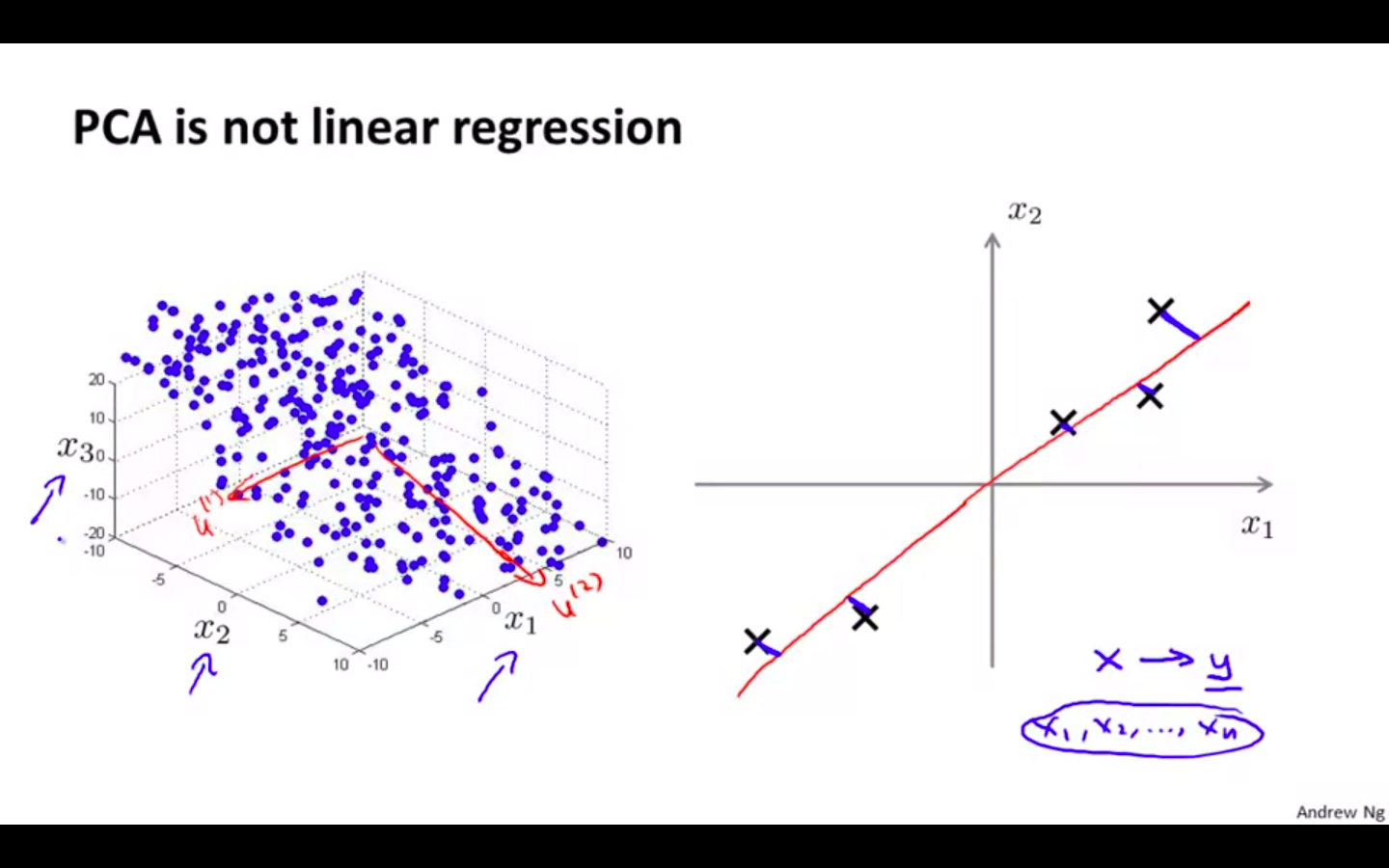
  • PCA is not Linear Regression

    • In linear regression, the error is draw 90 degree from the line to the data point

    • In PCA, the projection error is drawn at a angle from the line to the data point

    PCA vs LR.png PCA vs LR 1.png

Principal Component Analysis Algorithm

  • Data Preprocessing

    • Mean Normalisation

    Data Preprocessing.png

  • PCA Algorithm

    • Reducing dimension of data

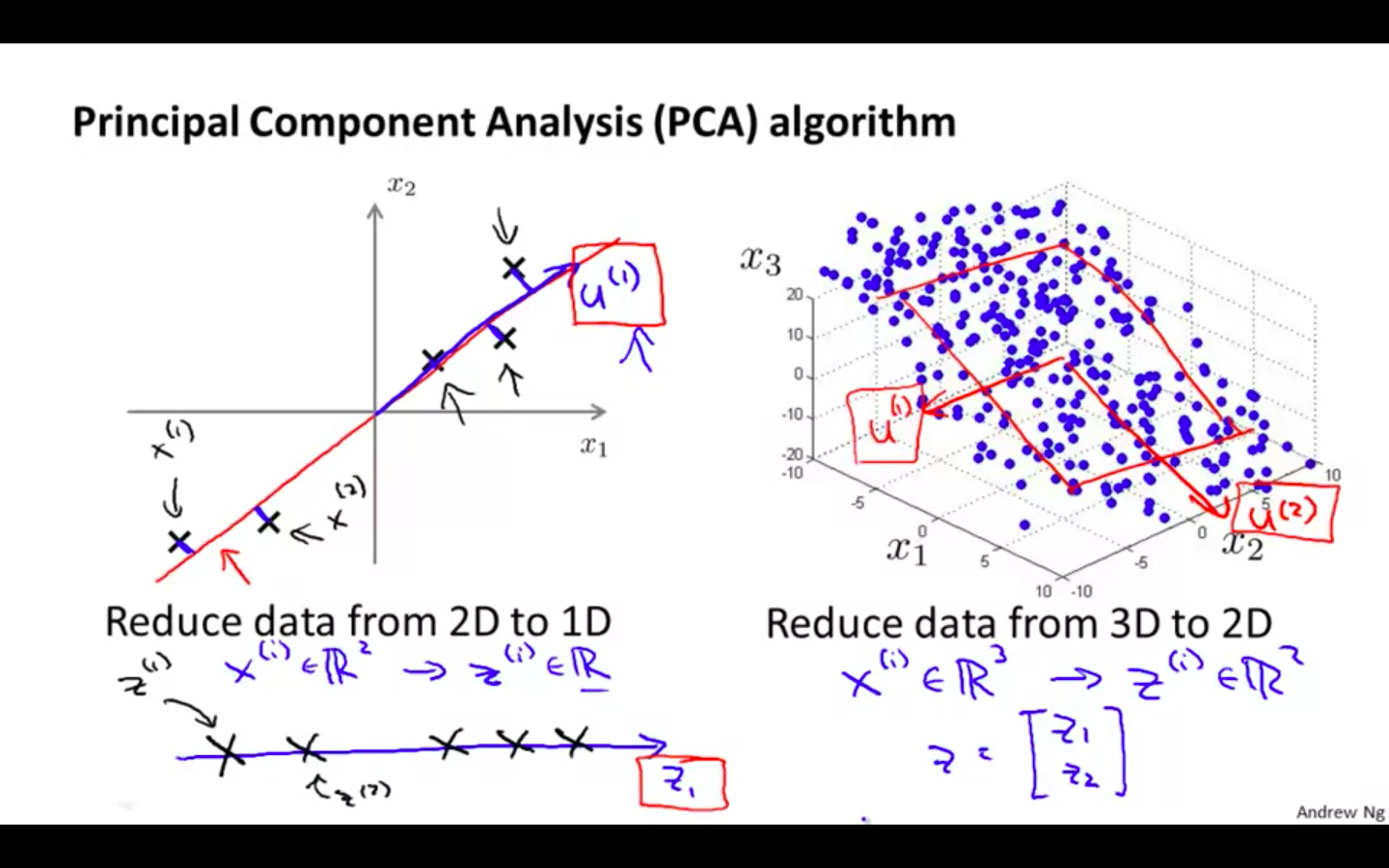
    PCA Algorithm.png

    • Compute ‘Covariance Matrix’

    • Compute ‘eigenvectors’ of matrix

    PCA Algorithm 1.png PCA Algorithm 2.png

    • Summary

    PCA Algorithm Summary.png

Applying PCA

Reconstruction from Compressed Representation

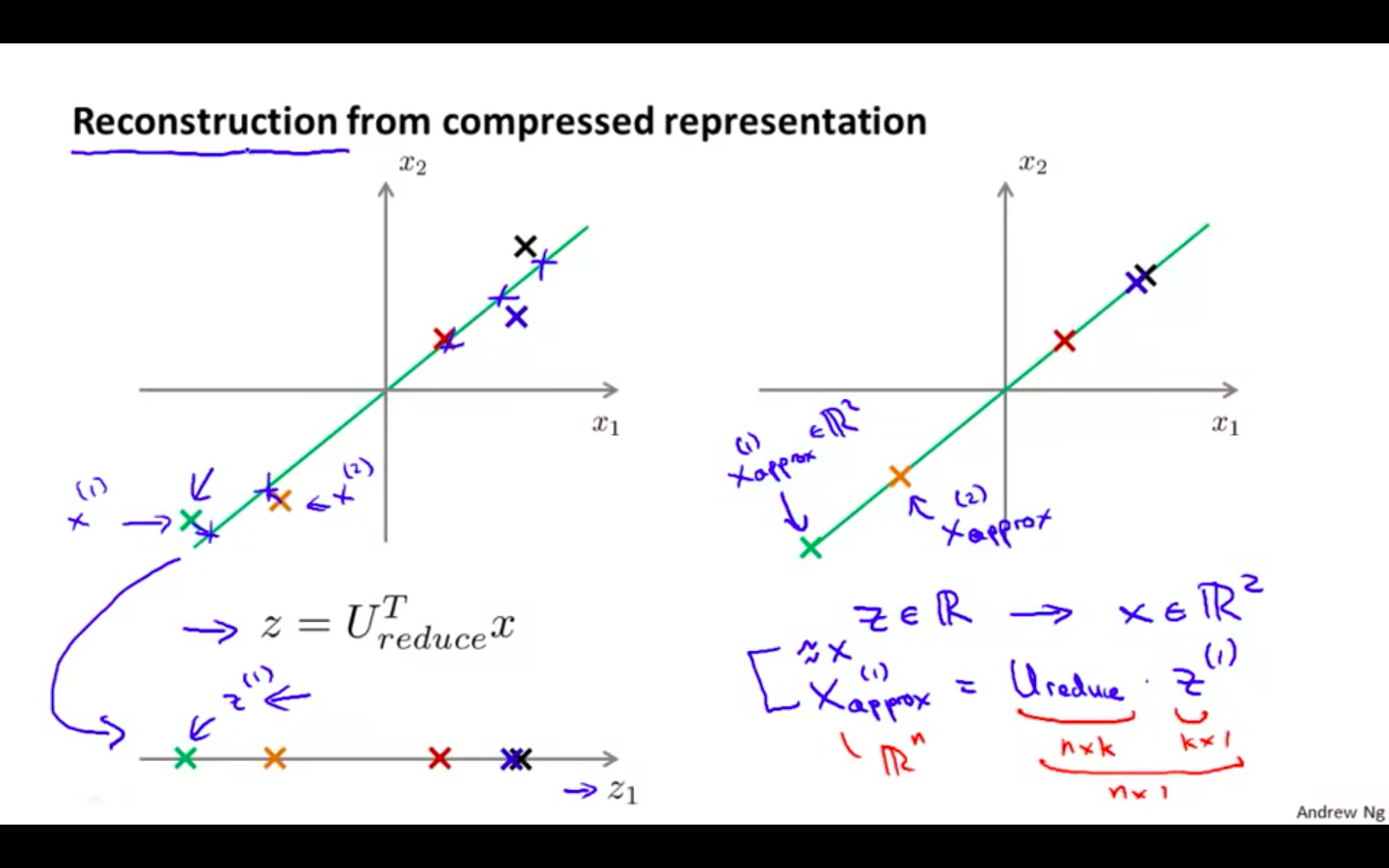
Reconstruction from Compressed Representation.png

Choosing the Number of Principal Components

  • Choosing k ( number of principal components )

    • Average squared projection error / Total variation in the data ≤ 0.01

    • 99 % of variance is retained

    Choosing k.png

  • Different Algorithms

    Choosing k 1.png

  • Recommended Method

    Choosing k Method.png

Advice for Applying PCA

  • Supervised Learning Speedup

    Supervised Learning Speedup.png

  • Applications

    • Compression

      • Reduce memory / disk needed to store data

      • Speed up learning algorithm

    • Visualisation

    Applications.png

  • Bad Use

    Bad Use.png

  • Where it shouldn’t be used

    More Bad Use.png

Lecture Presentation