Machine Learning By Andew Ng - Week 9

Density Estimation

Problem Motivation

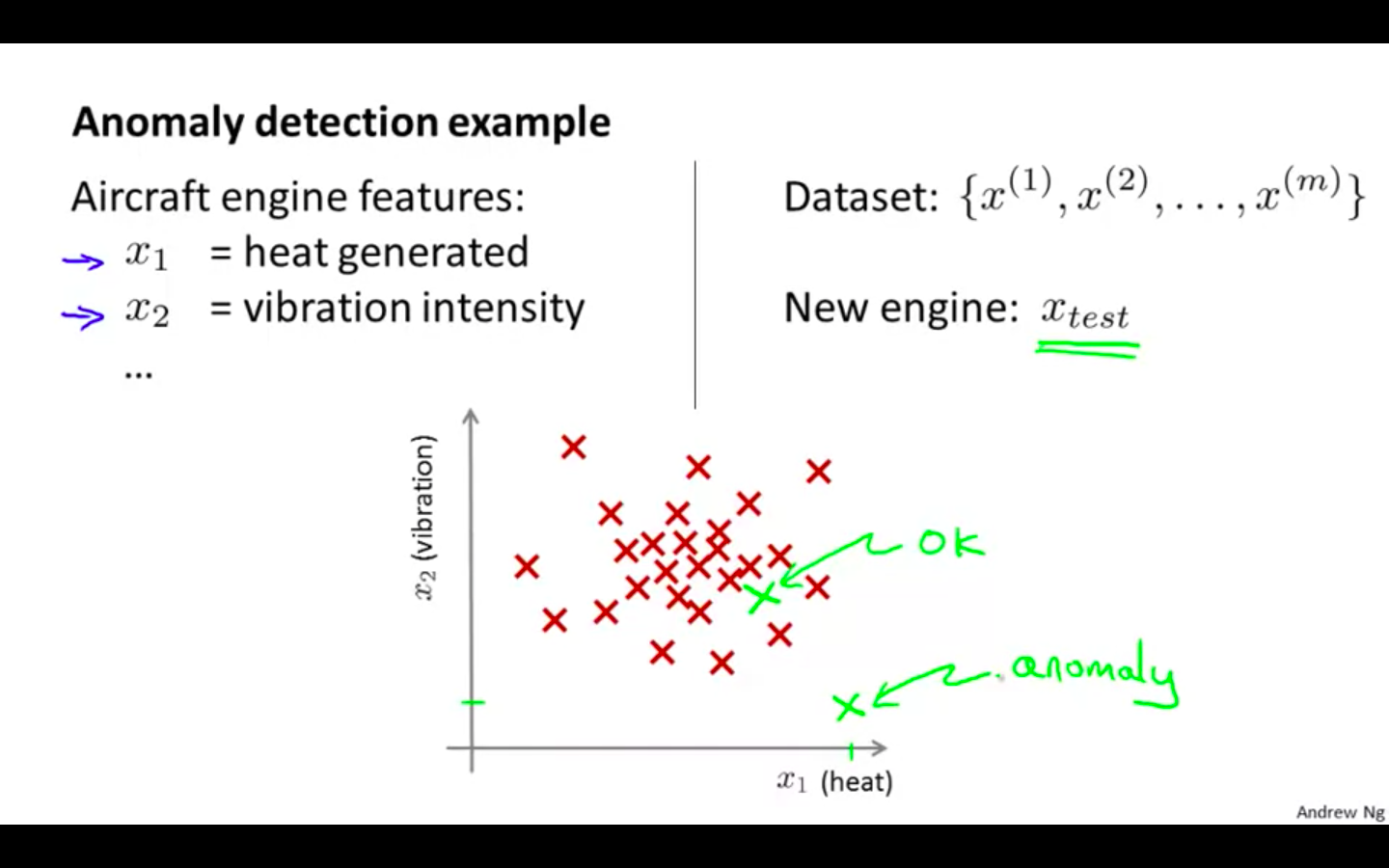
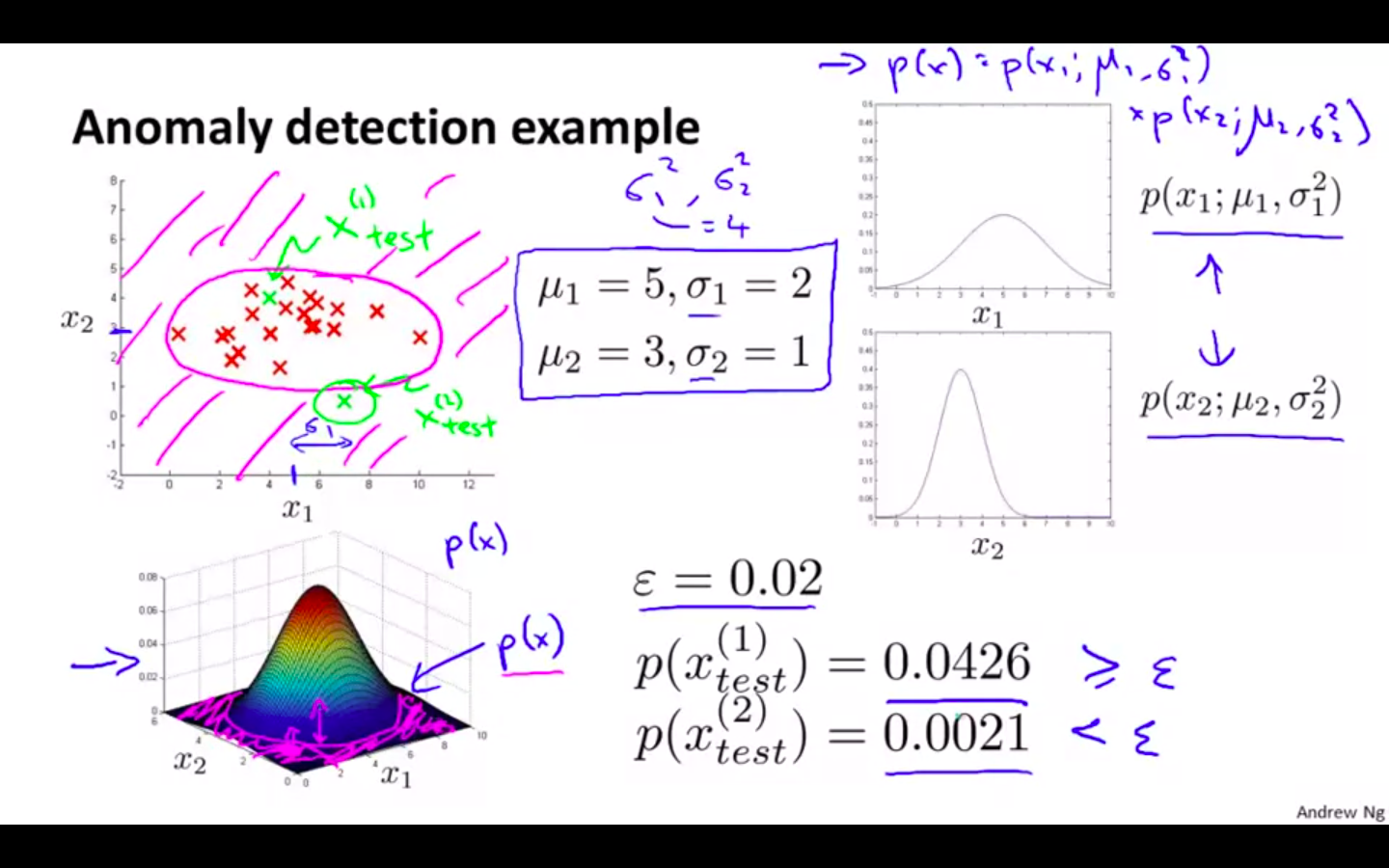
• Anomaly Detection Example

  • Plotting the dataset, and compare it with the new datapoint for its behaviour

  • If its in the same range as the dataset then the new datapoint is identified as ok

  • It its not in the same range as the dataset then the new datapoint is flagged as anomaly

  

• Density Estimation

  • If new datapoint is less than some value ( epsilon ) then flagged as anomaly

  • If new datapoint is equal to or more than some value ( epsilon ) then identified as ok

  

• Anomaly Detection Applications

  • Fraud Detection

  • Manufacturing

  • Monitoring computers in a data center

  

Gaussian Distribution

• Gaussian Distribution

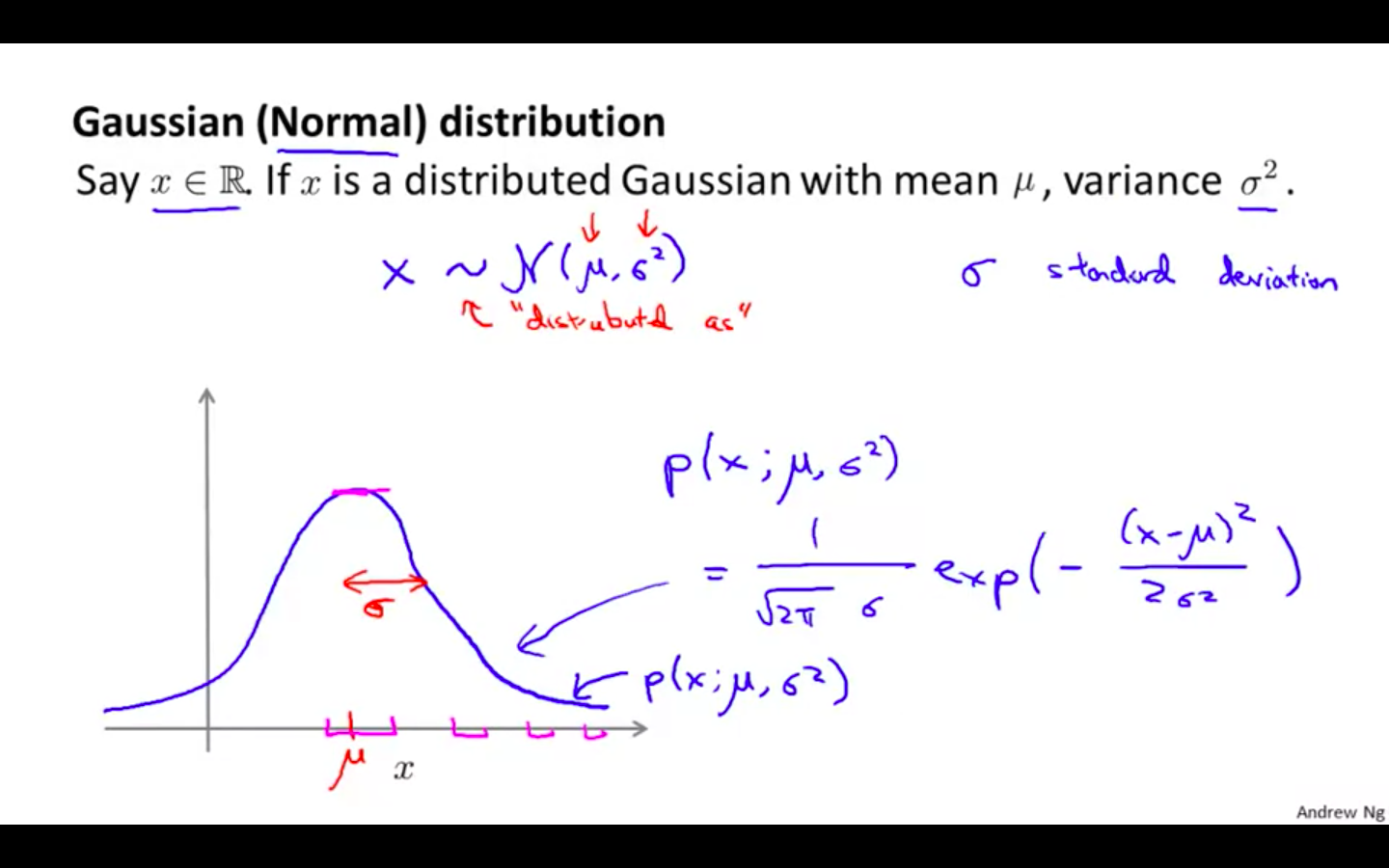
  • Say x belongs to Real Number.

  • If x is a distributed Gaussian with mean and variance

  

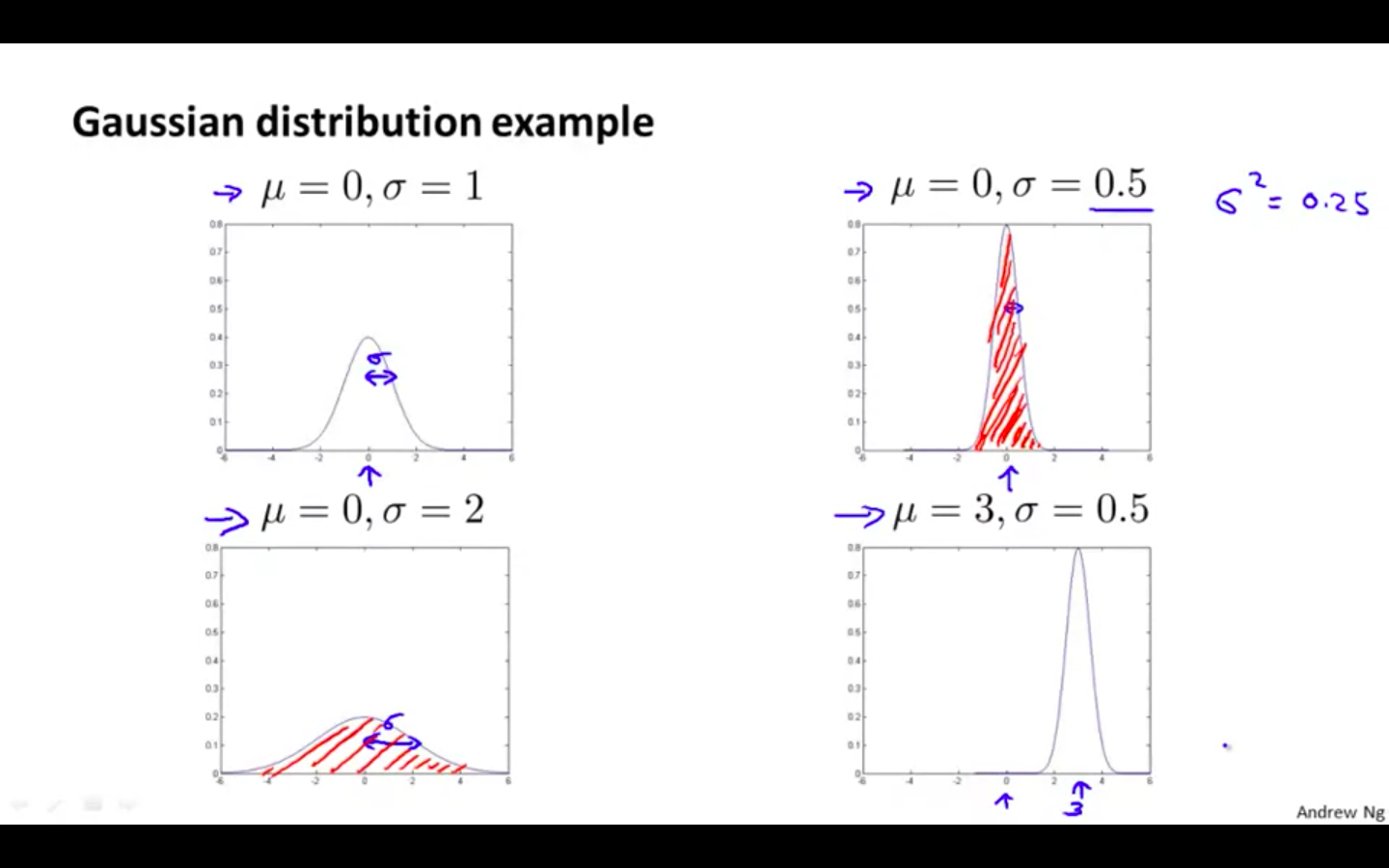
• Gaussian Distribution Examples

  

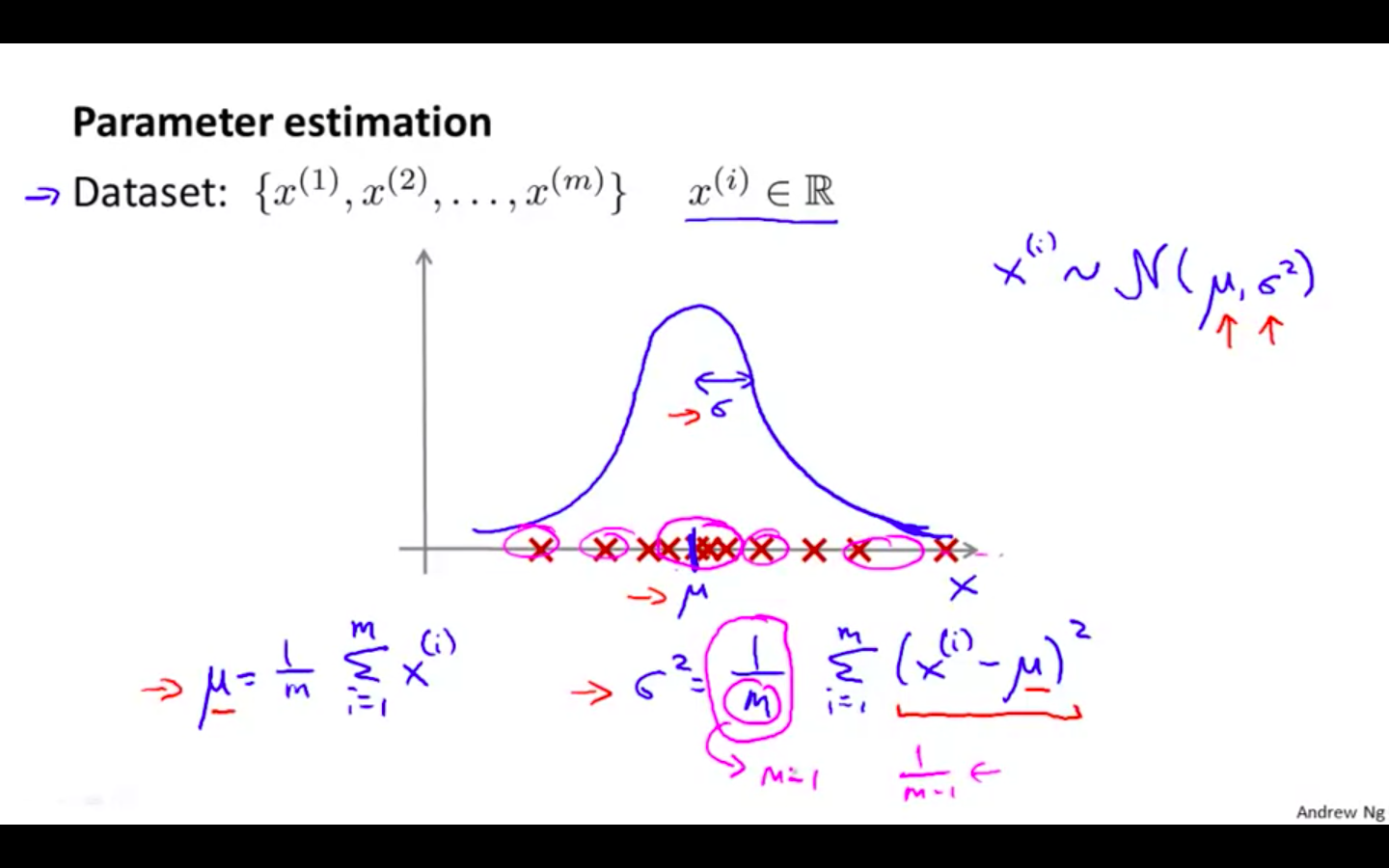
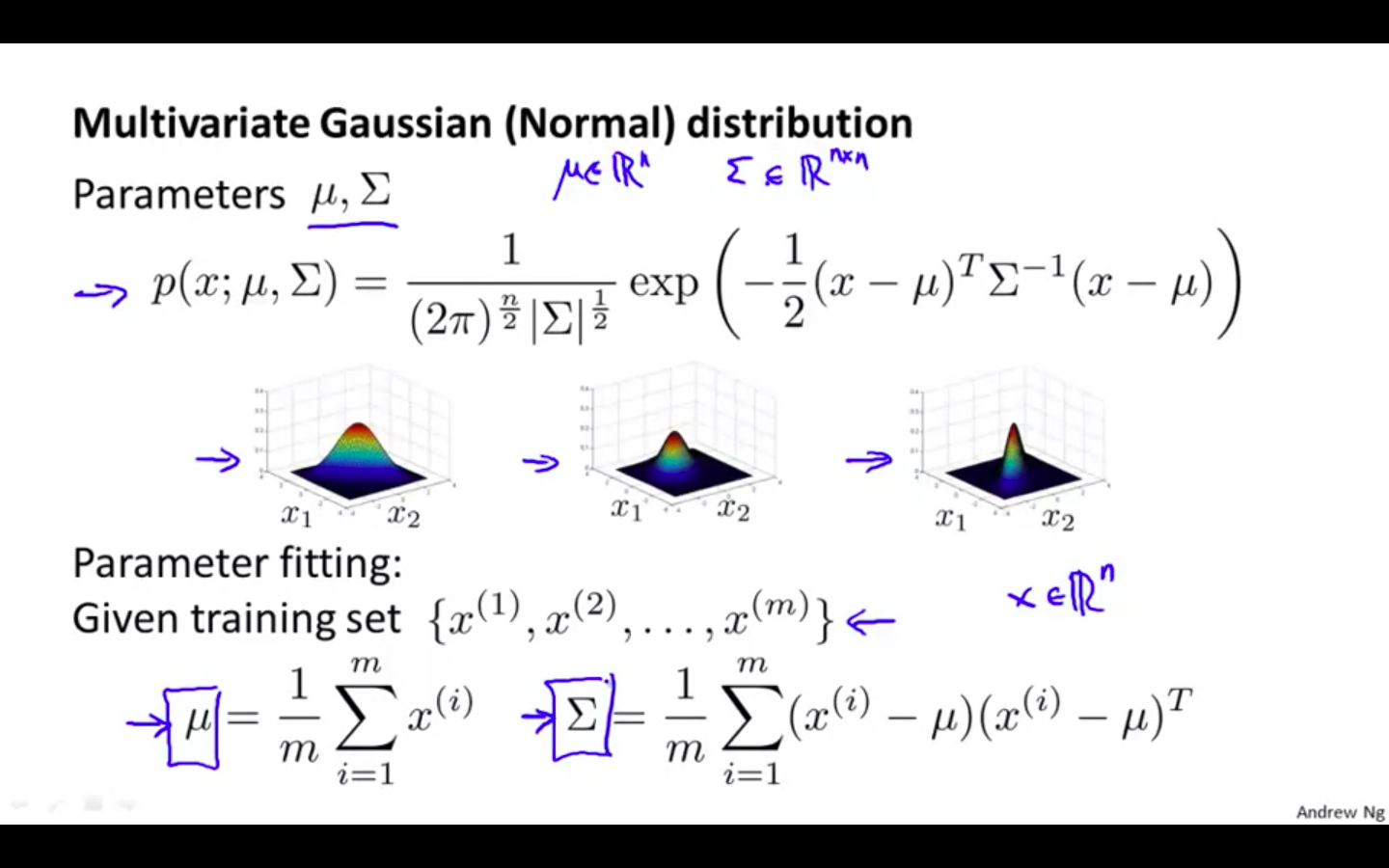
• Parameter Estimation

  • Finding mean and variance from the Gaussian Distribution

  

Algorithm

• Density Estimation

  • Big notation of pi indicates product

  

• Algorithm

  • Choose features x, that might be indicative of anomalous examples

  • Fit parameters - mean and variance

  • Given new example x, compute p( x )

  • p ( x ) ≥ epsilon ⇒ OK

  • p ( x ) < epsilon ⇒ Anomaly

  

• Anomaly Detection Example

  

Building an Anomaly Detection System

Developing and Evaluating an Anomaly Detection System

• Importance of Real Number Evaluation

  • When developing a learning algorithm ( choosing features, etc . ) making decisions is much easier if we have a way of evaluating our learning algorithm

  

• Data Split

  • 60 - 20 - 20 data split

  

• Evaluation

  • Evaluation metrics

    • True positive, false positive, false negative, true negative

    • Precision / Recall

    • F score

  • Use cross validation set to choose parameter epsilon

  

Anomaly Detection vs Supervised Learning

• Anomaly Detection vs Supervised Learning

• Anomaly Detection vs Supervised Learning Examples

Choosing What Features to Use

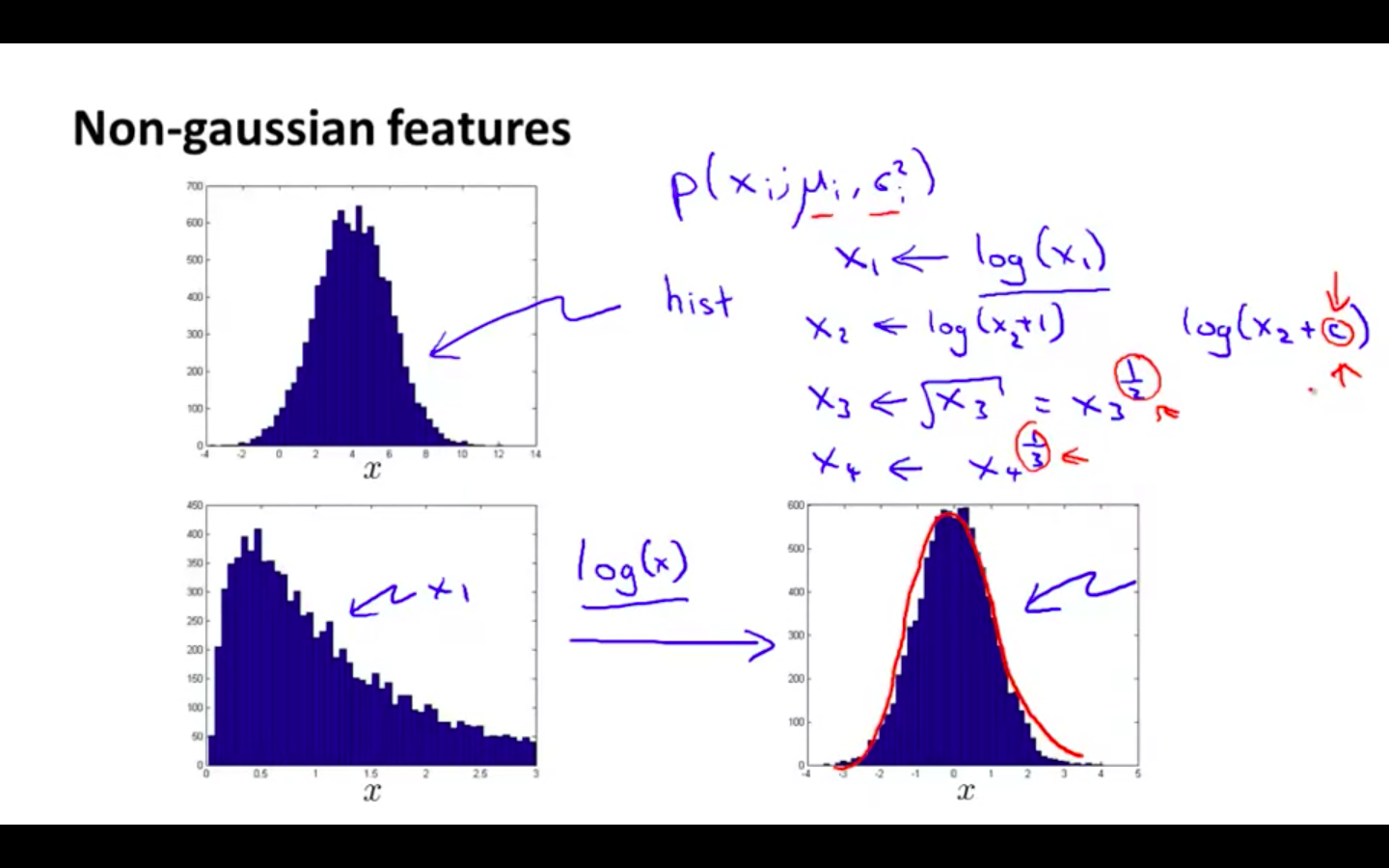
• Non Gaussian Features

  • Transform your non gaussian data to the form of gaussian by doing some operations on it and then feed it to the algorithm

  • It will work even if its not transformed, but it will gives less performance

  

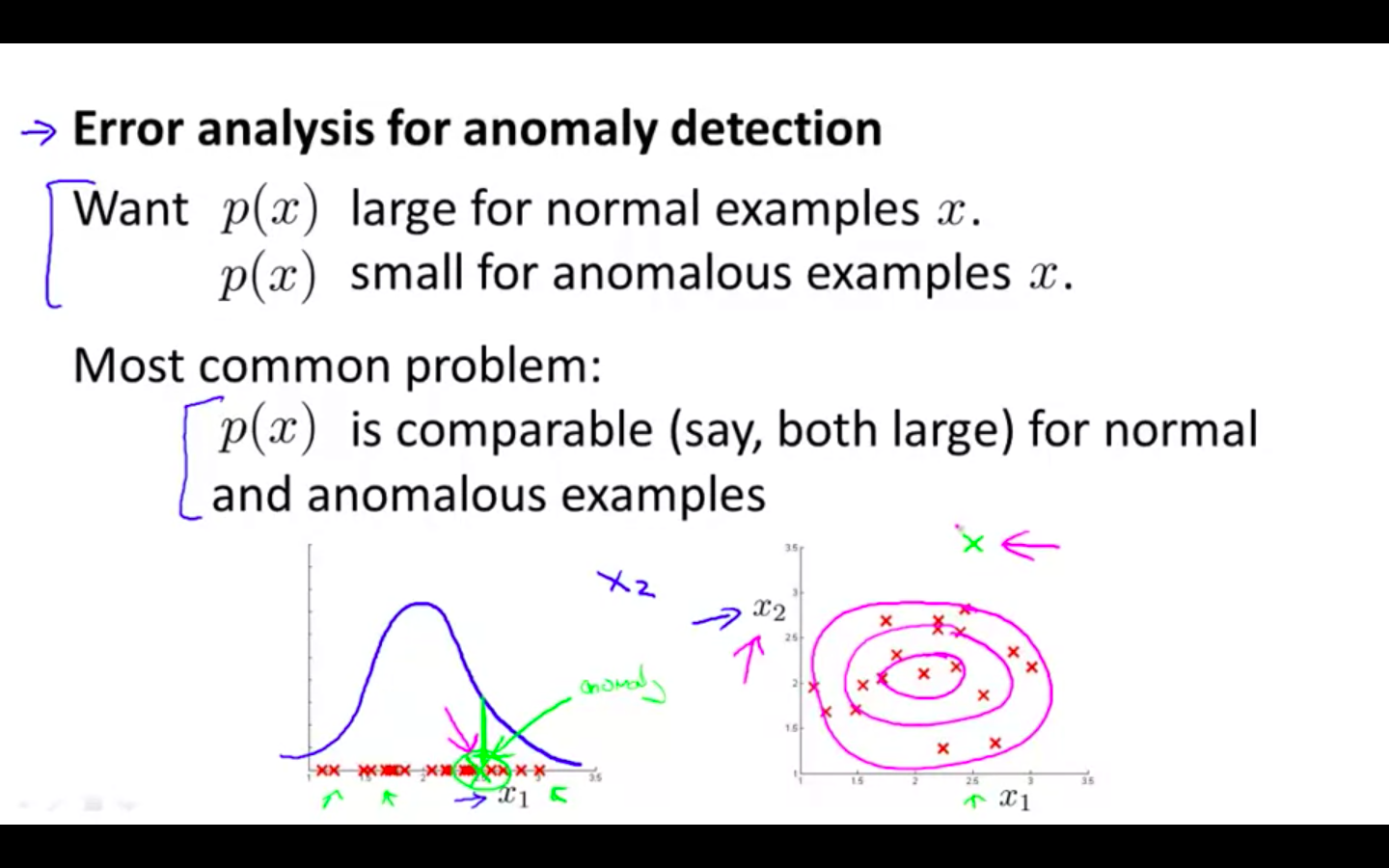
• Error Analysis

  • Find new features by analysing the mistake done by the algorithm in flagging anomaly

  

• Example

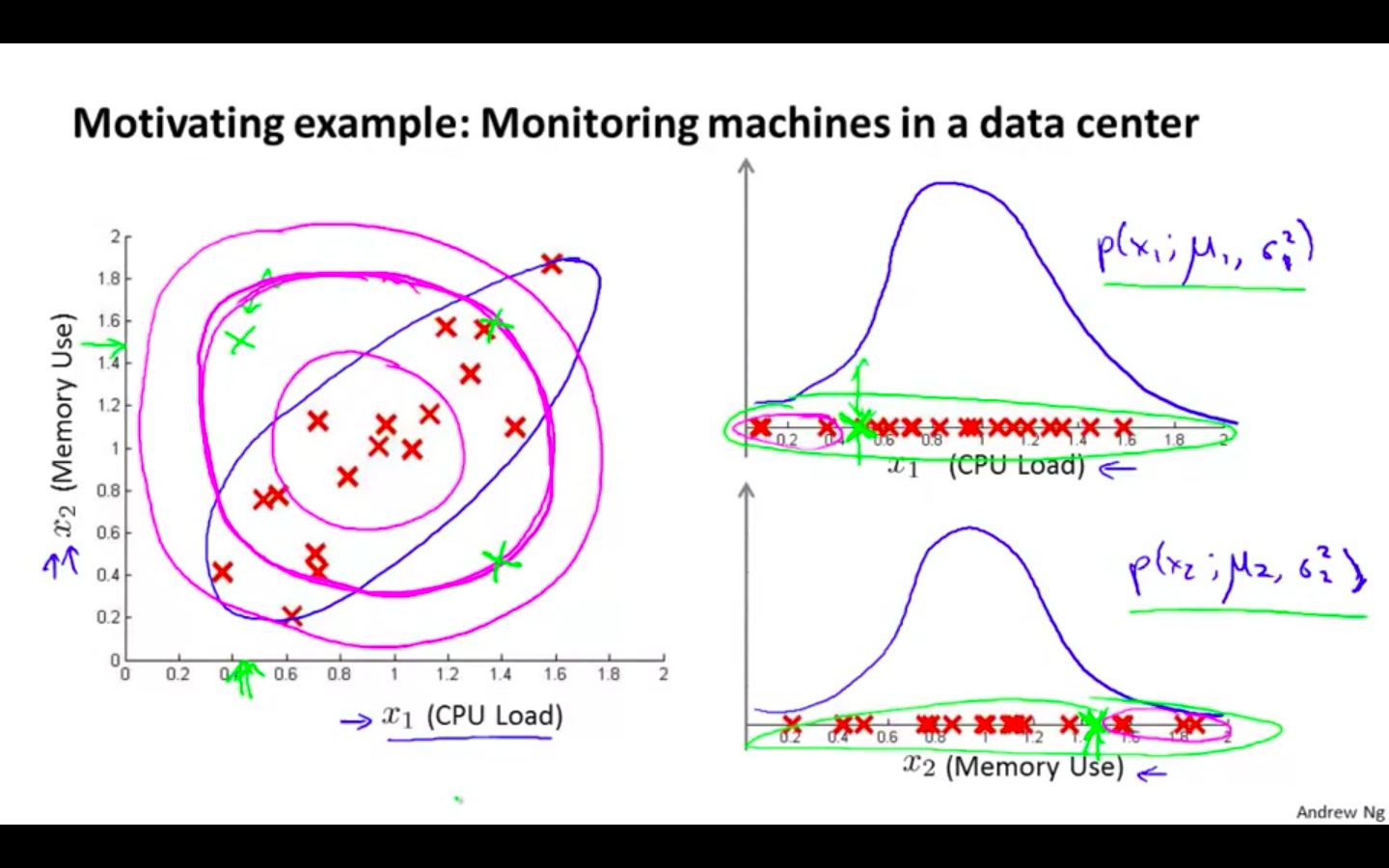
  • Monitoring computers in a data center

    • Choose features that might take on unusually large or small values in the event of anomaly

    • x1 = memory use of computer

    • x2 = number of disk accesses / sec

    • x3 = CPU load

    • x4 = network traffic

    • x5 = CPU load / network traffic ( new feature )

  

Multivariate Gaussian Distribution

Multivariate Gaussian Distribution

• Motivating Example

  • Monitoring machines in a data center

  

• Multivariate Gaussian Distribution

  • x belongs to real number

  • Don’t model p ( x1 ), p ( x2 ) …. separately.

  • Model p ( x ) all in one go

  • Parameters: mean, covariance matrix

  

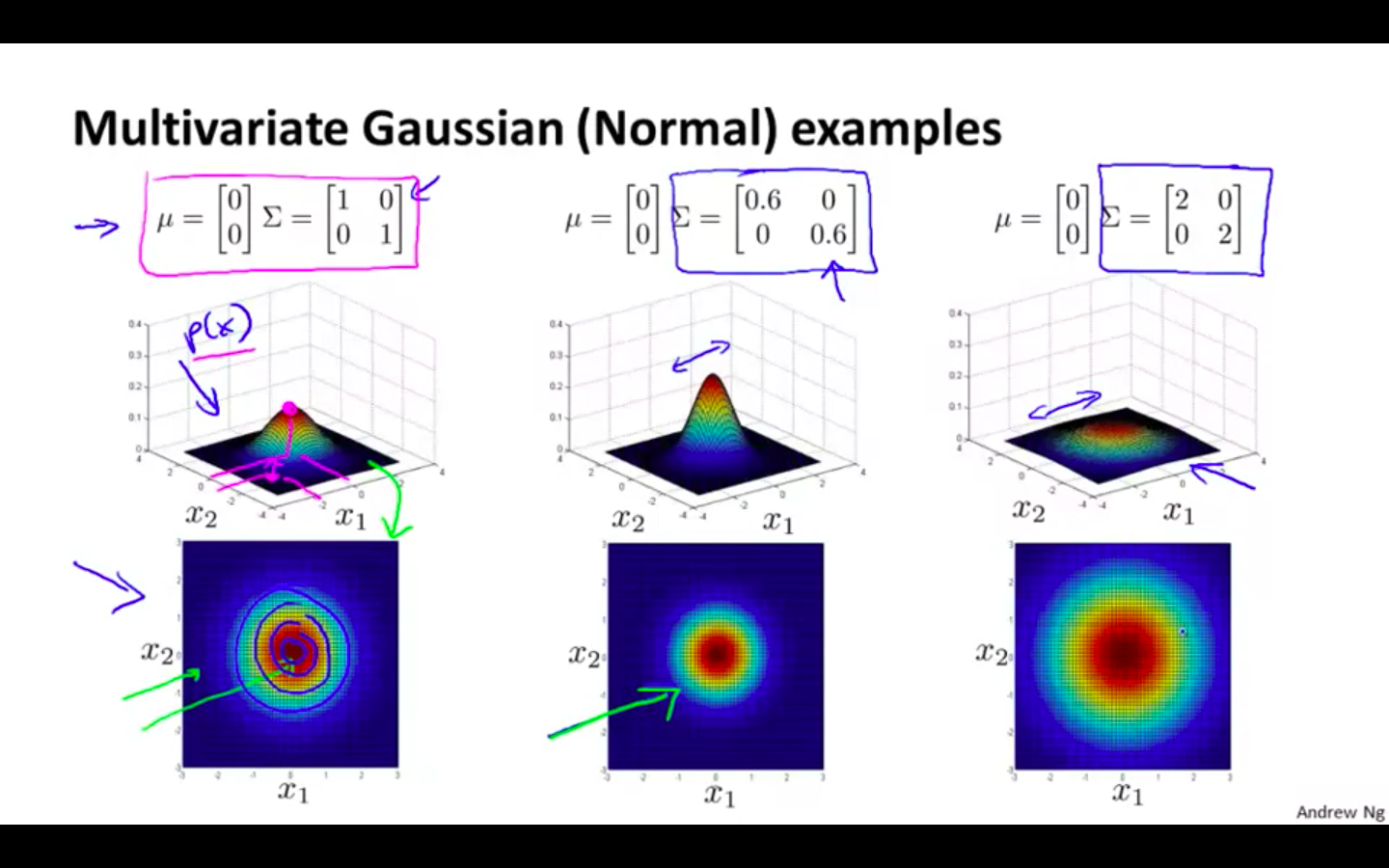
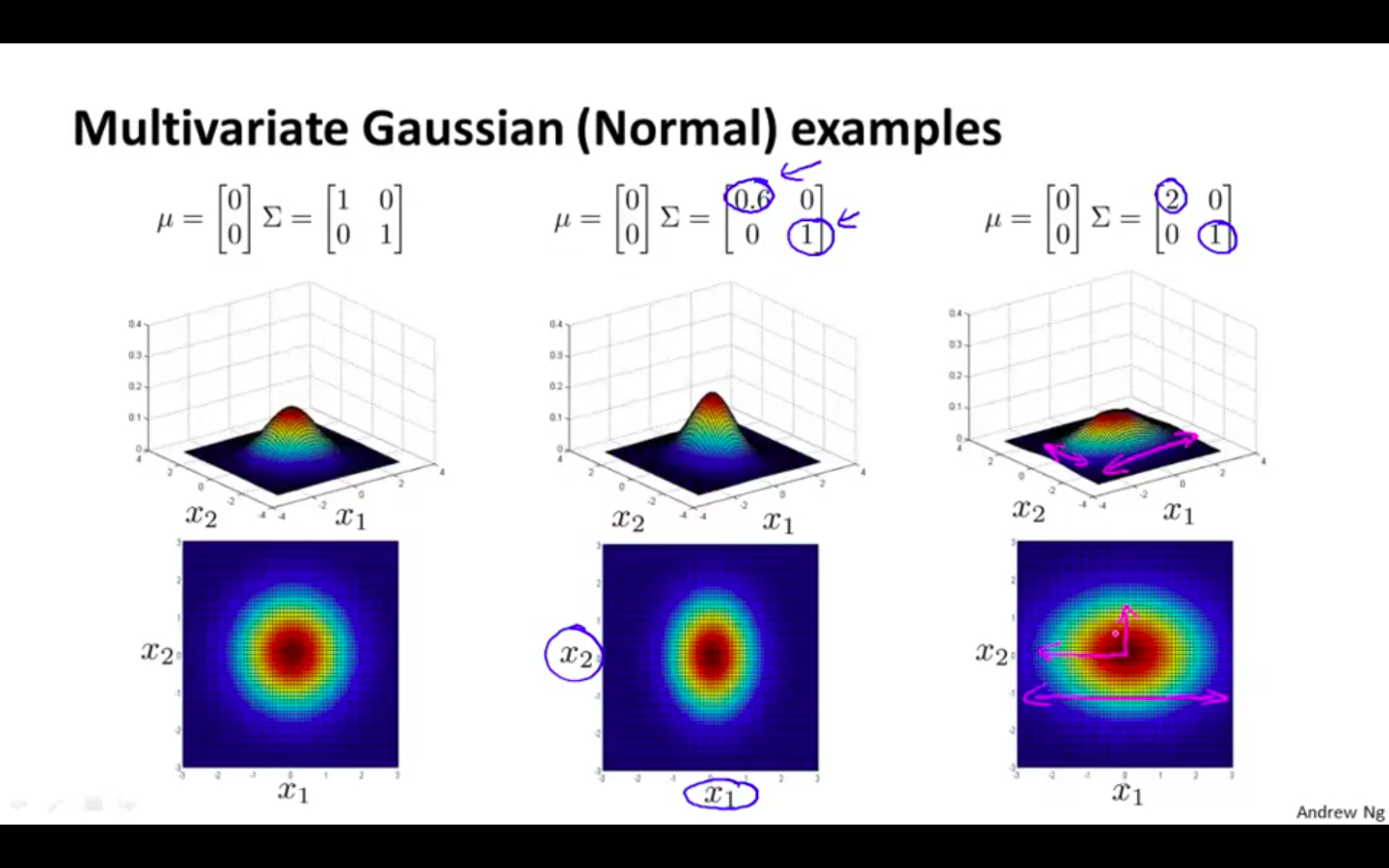
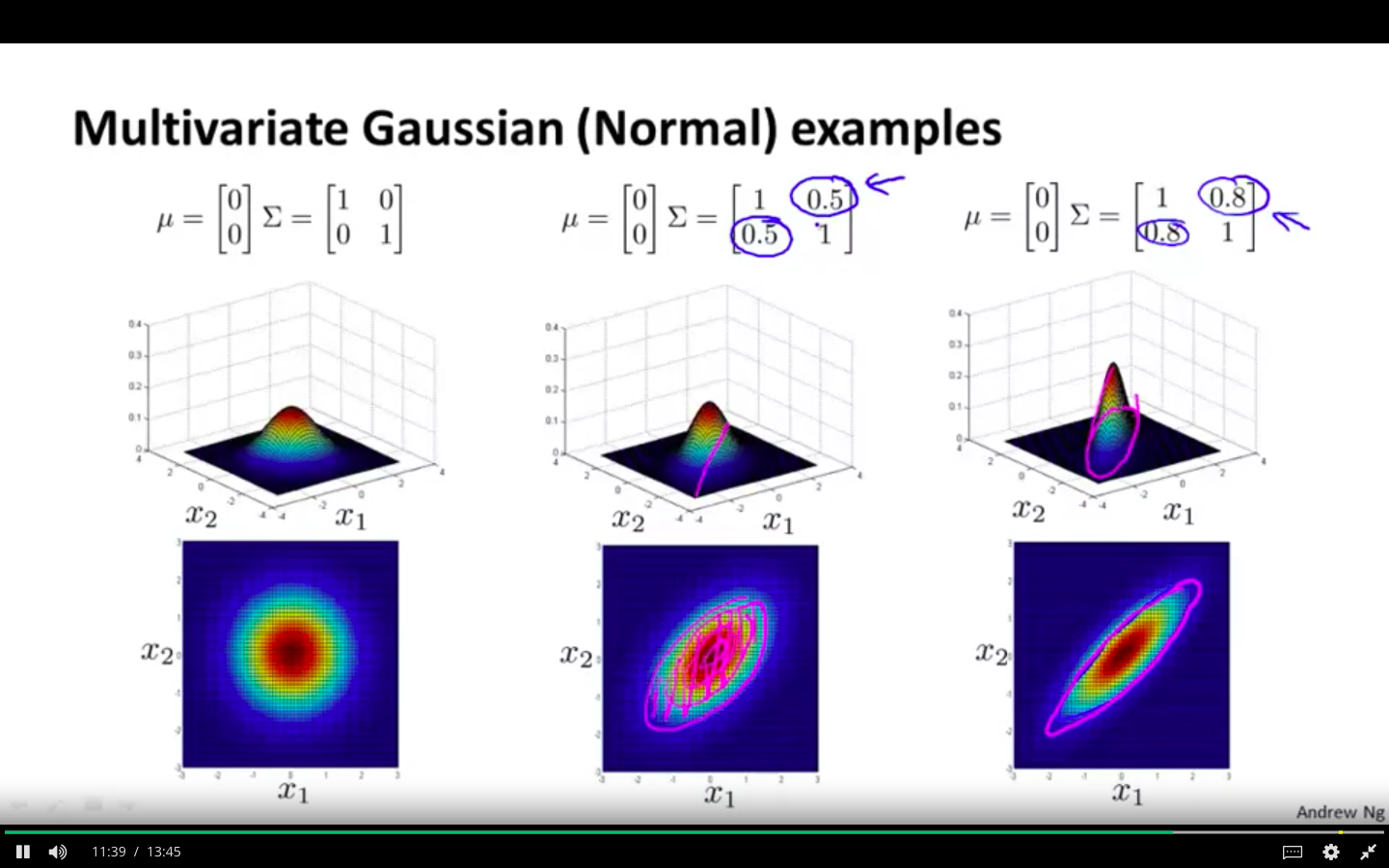
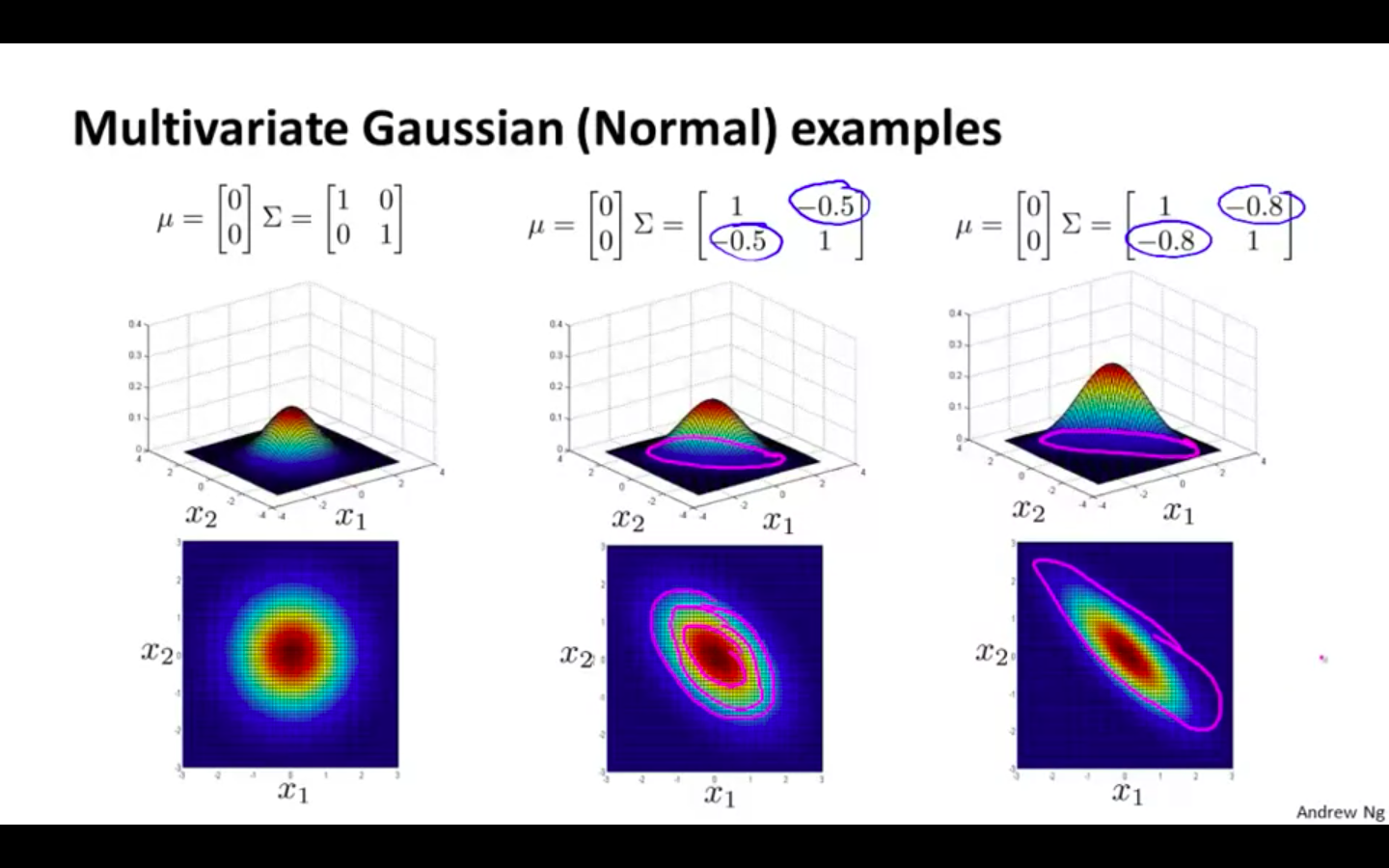
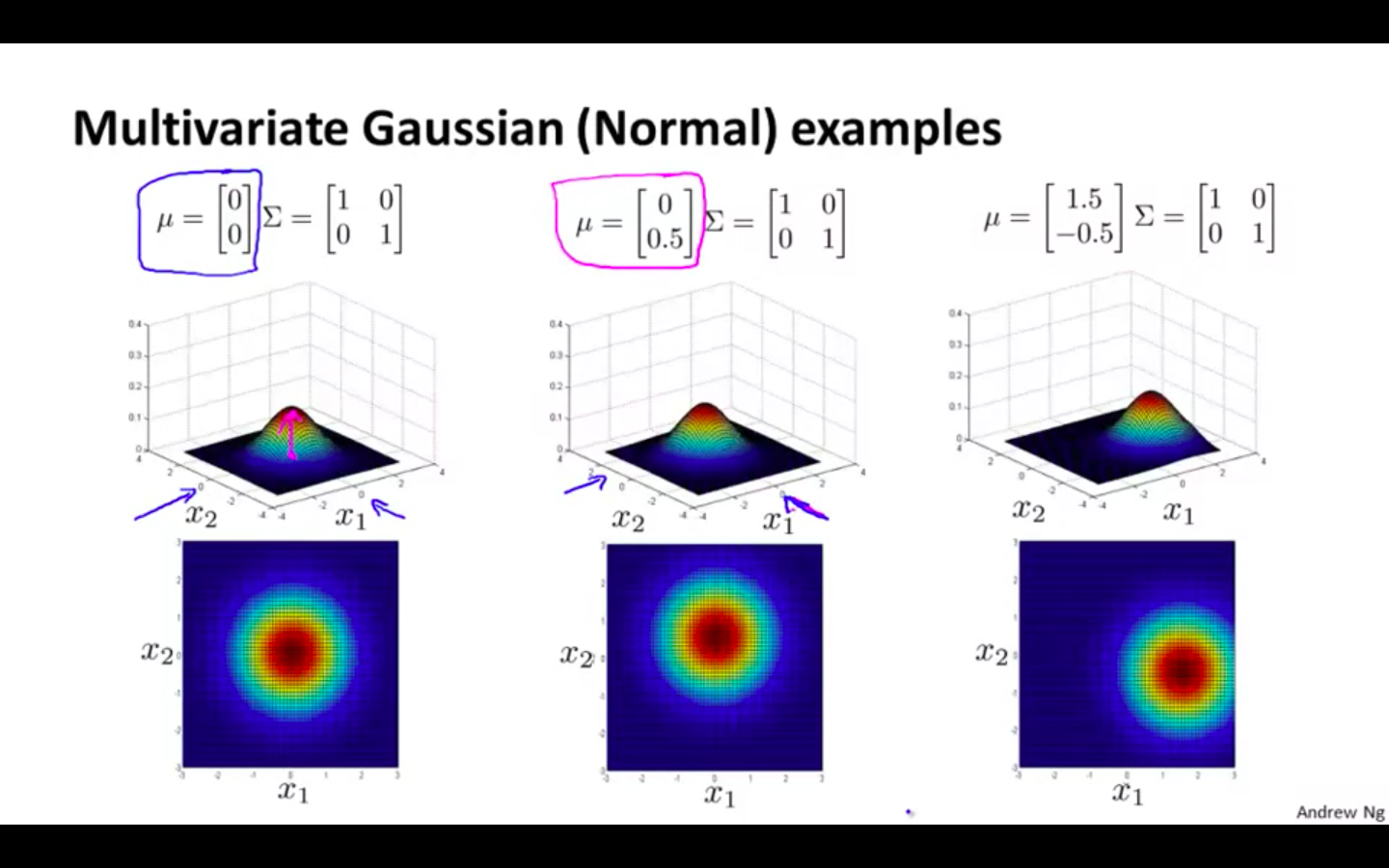
• Multivariate Gaussian Distribution Examples

  • Covariance matrix is altered

  • Only the first diagonal

  • Even alteration

  

  • Uneven alteration

  

  • Altering second diagonal evenly

  

  • Altering second diagonal values negatively

  

  • Altering the mean value

  

Anomaly Detection using the Multivariate Gaussian Distribution

• Multivariate Gaussian Distribution

  • Formula

    • Finding the parameters with the formula

    

  • Flow

    • Substituting the values of parameters in the formula

    

  • Relationship to the original model

    • It can proved as the special case of the multivariate gaussian distribution where it aligned with the axis

    

• Differentiation

• Original Model vs Multivariate Gaussian

Predicting Movie Ratings

Problem Formulation

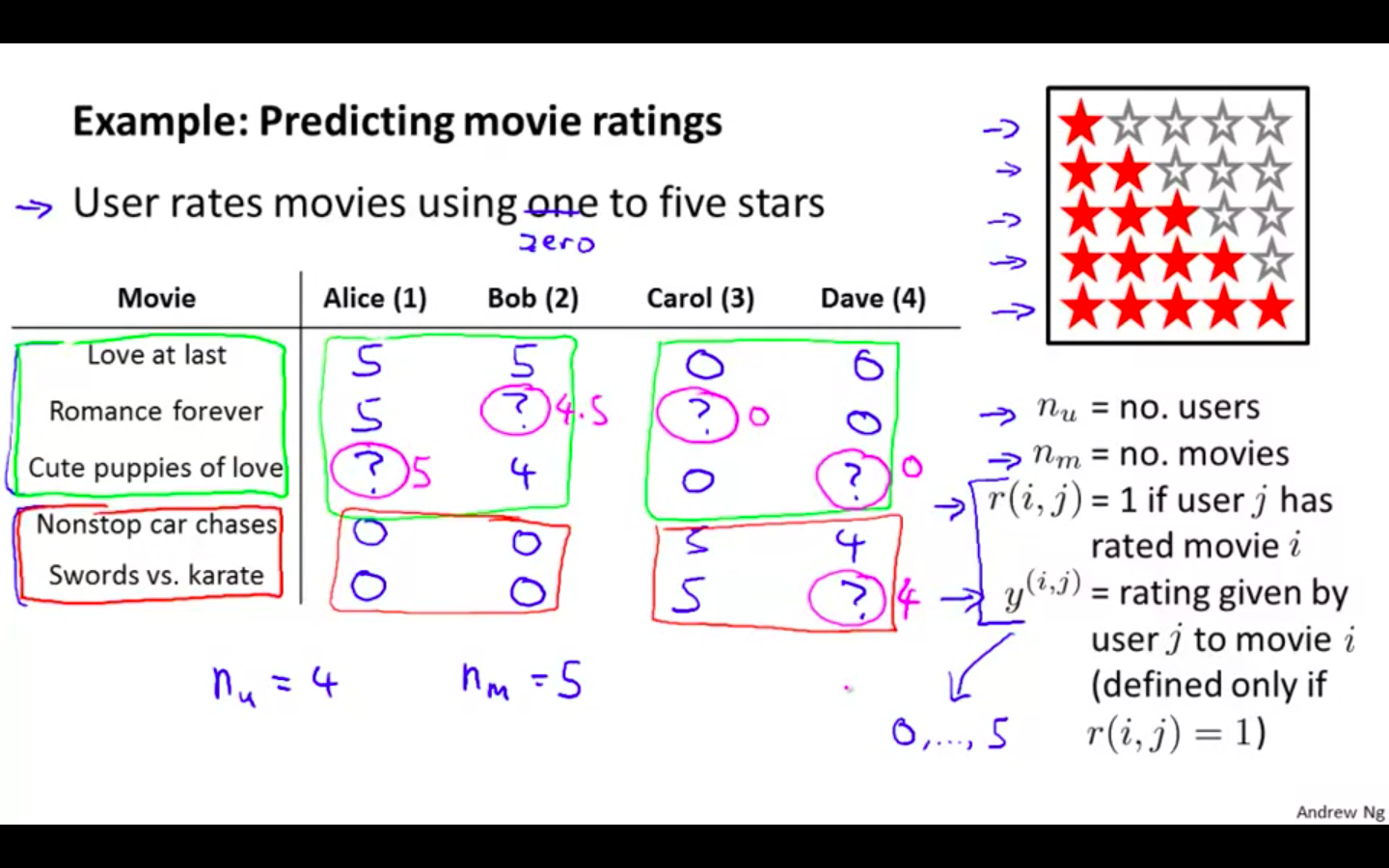
• Example

  • Predicting Movie Rating

    • n_u ⇒ no. of users

    • n_m ⇒ no. of movies

    • r ( i , j ) = 1 ⇒if user j has rated movie i

    • y ^ ( i , j ) ⇒ rating given by the user j to movie i ( defined only if r ( i , j ) = 1 )

  

Content Based Recommendations

• Content Based Recommender System

  • This is recommender system which uses one form of linear regression

  

  • Problem Formulation

    • r ( i , j ) = 1 ⇒if user j has rated movie i

    • y ^ ( i , j ) ⇒ rating given by the user j to movie i ( defined only if r ( i , j ) = 1 )

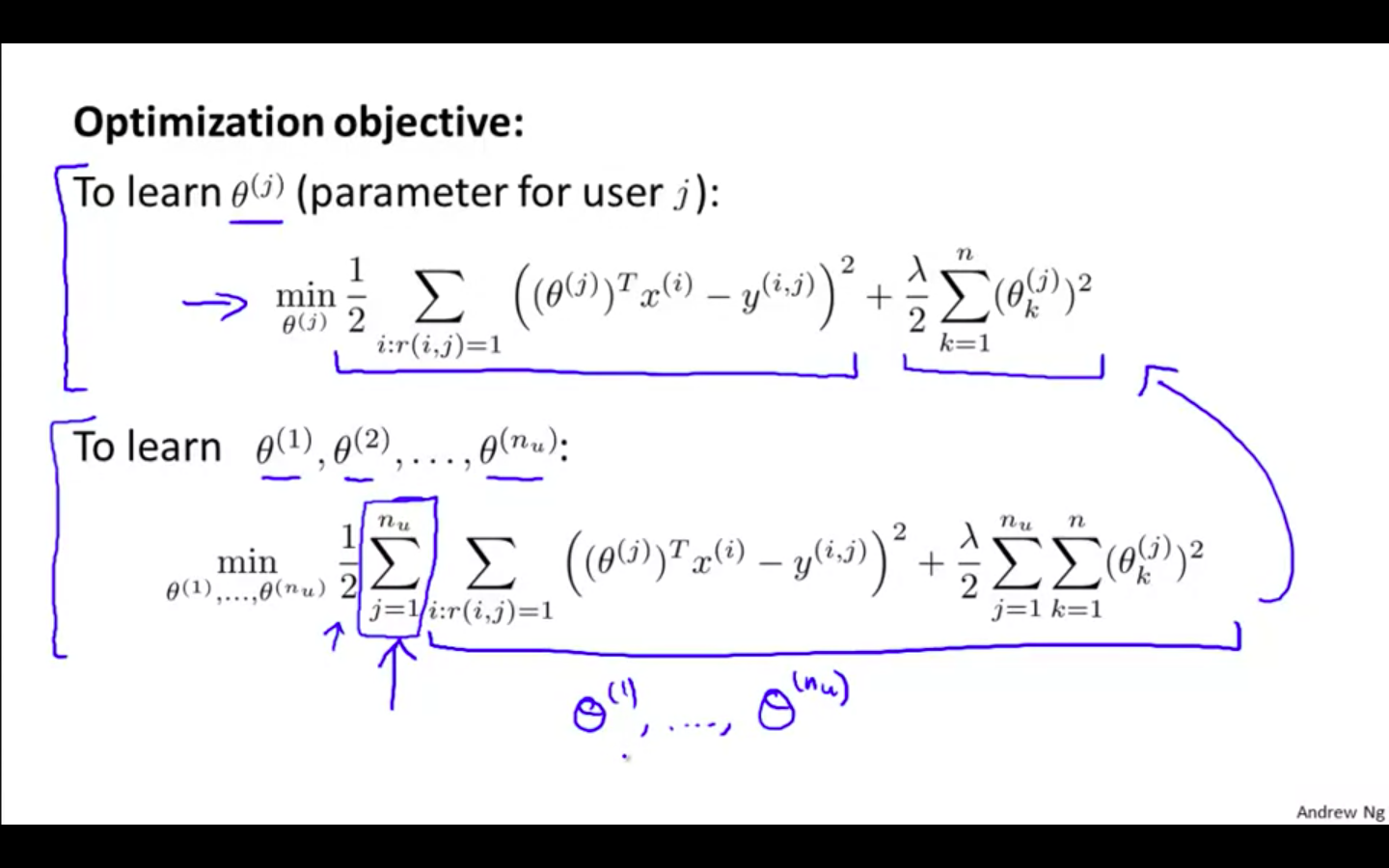
    • theta^j ⇒ parameter vector for user j

    • x ^ i ⇒ feature vector for movie i

    

  • Optimisation Objective

    

  • Gradient Descent Update

    

Collaborative Filtering

Collaborative Filtering

• Problem Motivation

  

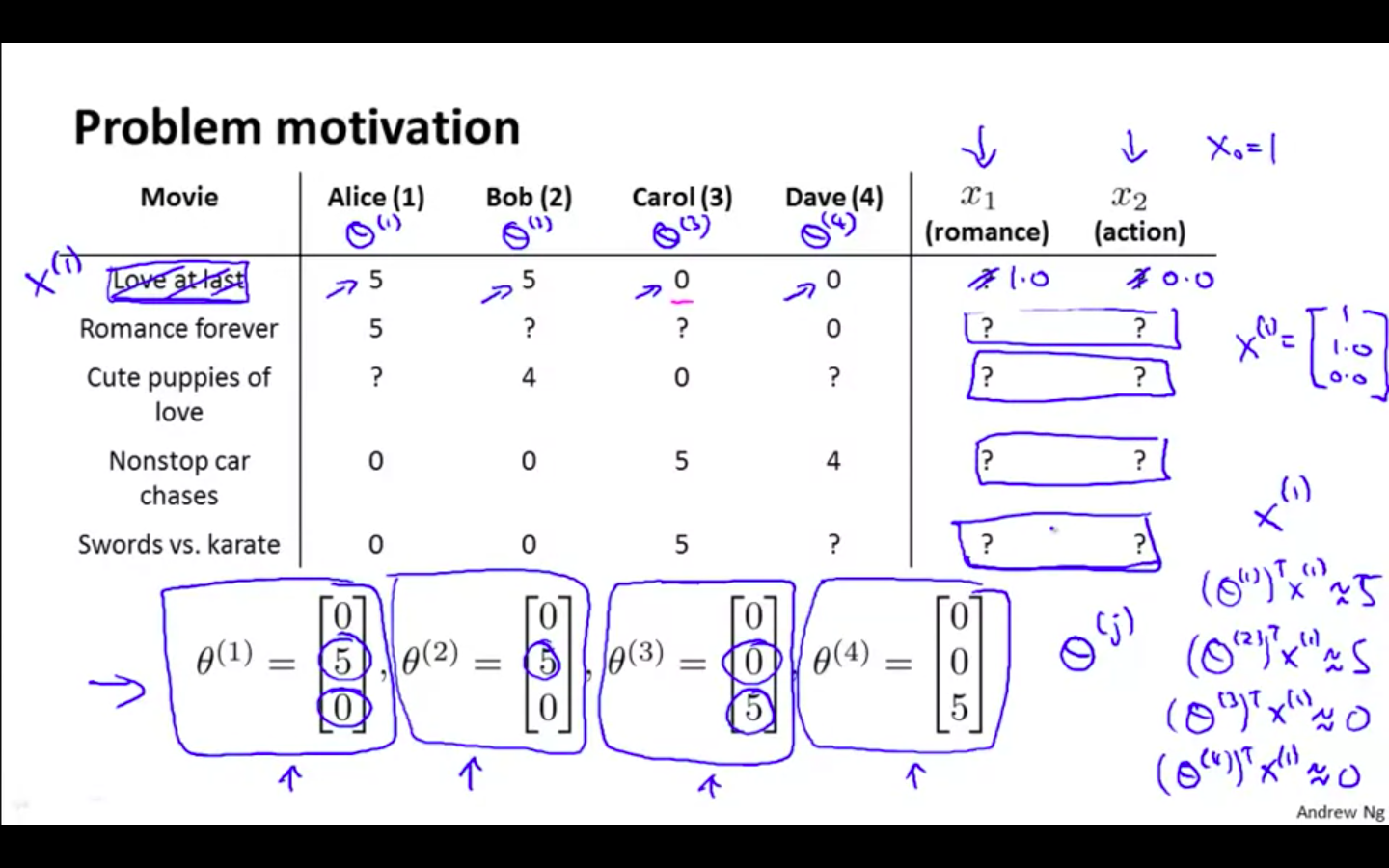
• Optimisation Algorithm

  

• Collaborative Filtering

  • Given x, to learn theta

  • Given theta, to learn x

  • Continuous updating both values

  

Collaborative Filtering Algorithm

• Collaborated Formula

  • Formula has been concatenated of the earlier formula

  

• Collaborative Flow

  • Initialise x and theta to small random values

  • Minimise J ( x , theta ) using gradient descent ( or any other advance optimisation algorithm )

  • For a user with parameter theta and a movie with ( learned ) features x, predict a star rating of theta^T

  

Low Rank Matrix Factorisation

Vectorisation: Low Rank Matrix Factorisation

• Collaborative Filtering

  

• Low Rank Matrix Factorisation

  

• Finding Related Movies

  

Implementation Detail: Mean Normalisation

• Users who have not rated any movies

  

• Mean Normalisation

  

Lecture Presentations